http://dx.doi.org/10.15649/2346030X.875

Implementación de la Técnica de Correlación de Imágenes Digitales con Software Libre.

Digital Image Correlation Technique Implementation with Open Software.

Iván Mauricio Castillo-González¹ Adrián Eduardo Peñaranda-Dominguez² Jorge Guillermo Díaz-Rodríguez³

¹ Universidad Santo Tomás, Colombia.
² Universidad Santo Tomás, Colombia.
³ Universidad Santo Tomás, Colombia. E-mail: jorgeguillermo12@ustabuca.edu.co Autor de correspondencia

Recibido: 29 de junio de 2020
Aceptado: 31 de octubre de 2020

Atribución 4.0 Internacional (CC BY 4.0)

Resumen— Hoy en día, la medición experimental de esfuerzos se hace por medio de técnicas que entregan campos completos de deformación o de la diagonal principal de una matriz de esfuerzos. La técnica de Correlación de Imágenes Digitales (DIC en idioma inglés) entrega desplazamientos del campo de visión mediante el análisis de fotografías digitales antes y después de una carga. Existen sistemas comerciales, que tienen un elevado costo, y sistemas de código abierto y gratis pero que no tienen soporte; esto hace que su implementación presente dificultades. El articulo trata de la apropiación de la técnica DIC usando software de código abierto. Para esto, se hicieron algunos ensayos de medición y se compararan con soluciones analíticas para evaluar la precisión de la medición experimental. Resultados se comparan con análisis por elementos finitos encontrando que, para dar mediciones cualitativas, que puede ser el caso de demostraciones, un lente no muy especializado puede ser útil, mientras que para mediciones cuantitavas se requieren de acercamientos en un plano focal cercano sólo dados por lentes macro.

Palabras clave:DIC, caracterización de materiales; medición de tensiones; mecánica experimental, análisis de tensiones.

.

Abstract —Nowadays, experimental stress and strains measurement is done by means of techniques that deliver whole fields of either displacement or stress range or the sum of the main diagonal of a stress tensor. The Digital Image Correlation (DIC) technique delivers orthogonal displacements within the field of vision through the analysis of digital photographs before and after an applied load. There are high cost commercial systems, and open source systems which are free of use and distribution but that do not have support; which makes its implementation rather difficult. The article deals with the appropriation of the DIC technique using DIC open source software. For this, some measurements were made and compared with analytical solutions to evaluate the precision of the experimental measurement. The best experimental results are compared with FEM simulations. It was found that commercial lenses can give qualitative measurements, i. e. for educational or illustrative purposes, whereas a macro lens is needed for quantitative measurements.

Keywords: DIC; materials characterization; stress measurement; experimental mechanics; stress analysis.

La técnica de Correlación de Imágenes Digitales (DIC) es una técnica experimental óptica no intrusiva que utiliza el valor de gris de un pixel para realizar una correlación de posición de dicho pixel entre un estado cargado y otro de referencia, generalmente sin carga. Al encontrar la ubicación en la imagen deformada permite obtener el campo completo de desplazamientos en la superficie de la probeta en ensayo [1].

La técnica nació en la universidad de North Carolina en 1982 [2] y se ha expandido rápidamente a la par del avance del poder de cómputo [1]. La técnica requiere un alto contraste en la muestra por lo que usualmente se pinta con un fondo blanco sobre el cual se aplican puntos negros muy finos [3]. Hoy en día existen por lo menos 4 grandes proveedores de soluciones integradas (hardware y software), una conferencia internacional anual dedicada a reportar avances en la técnica y su uso (iDics), así como competencias patrocinadas por la Sociedad Americana de Mecánica Experimental. De estas competencias han resultado software de Correlación de Imágenes Digitales de código abierto (Matlab ® [4], software libre como GOM y versiones académicas como DIC-edu de Correlated Solutions ®). Finalmente, otra alternativa para realizar mediciones de campo completo es usar un abordaje como el descrito en [5]. Allí no se usaron puntos aleatorios como en DIC, pero se usa un mismo tipo de comparación entre una posición de referencia y una deformada. Esta forma tiene la desventaja que se requiere conocer con antelación los puntos a medir para no atiborrar de puntos innecesarios el campo de visión. Adicionalmente, se deben mencionar otras dos opciones de software libre que no han sido evaluadas. Py2DIC [6] que fue liberado cuando ya se habían realizado los ensayos y [7] que está destinado a procesar mediciones de campos de desplazamientos obtenidos por tomografía de rayos X. Estos dos últimos escritos en Python. Finalmente, una propuesta novedosa [8] apunta a obtener campos tridimensionales con una sola cámara al hacer una partición de luz tomada desde puntos focales diferentes realizados con longitudes de onda diferentes (diferente color).

Algunos trabajos han comparado software de código abierto con versiones comerciales obteniendo resultados bastante cercanos [9]. Ncorr utiliza el solucionador no lineal de Gauss-Newton de composición inversa (ICGN) [4] que es rápido, robusto y preciso en la medición de desplazamiento en comparación con los esquemas clásicos de Newton Raphson o Forward Additive. Los gradientes de deformación unitaria pueden calcularse utilizando técnicas numéricas como Newton Raphson (NR), Quasi-NR, el algoritmo de Levenberg-Marquart (LM) [1] o Algoritmos Genéticos. El error en los campos de tensión estimados que usan NR o AG es de orden superior y limita su uso solo para valores de tensión aproximadamente mayores de 0.010 [3]. Para este caso, los AG no son recomendados debido a su alto costo computacional [10].

Se pueden obtener medidas de hasta 0.05 mm o menos usando soluciones comerciales las cuales incluyen cámaras de alta resolución, velocidades de obtención de cuadros de más de 25 fps (frames per second) y lentes de alto acercamiento a distancias focales cortas [3], [11]. El costo de estos sistemas es proporcional a la resolución y magnificación de los lentes, llegando hasta los U$35.000 para sistemas 2D y hasta U$70.000 para sistemas de medición 3D.

Otras implementaciones de sistemas DIC, o variantes, de bajo costo y aplicaciones se pueden encontrar en [12] en donde se usó un sistema DIC para realizar mediciones en fluidos, [13] y [14], [15] en donde se usó la técnica en materiales ortotrópicos, en [16] se miden extensiones de la muñeca y antebrazo, mediciones a altas tasas de [17] deformación, mediciones de grietas en 2D y 3D [18]–[25], mediciones a escalas bastante pequeñas  [17], [24], [26] o a de mayor tamaño como puentes [27] e incluso el uso de los campos obtenidos se ha usado recientemente [28] para alimentar algoritmos de detección de bordes, y muchas más aplicaciones.

Este paper muestra cómo se implementó un sistema de medición de desplazamientos usando un algoritmo de código abierto [4]. El artículo se alinea con recientes opiniones sobre el uso de técnicas de ingeniería en Colombia como computación, pero aplicada a comportamiento de materiales [29]. Finalmente, el artículo da detalles de preparación de muestras y compara de resultados usando diferentes lentes con técnicas numéricas.

La técnica DIC fue ideada en 1982 en la Universidad de Carolina del Sur, donde una serie de papers [2] [30] describieron un método para estimar la deformación de una probeta fotografiada bajo deformación y mostraba cómo calcular los desplazamientos y rotación de cuerpo rígido [31] y otro más mostraba como calcular factores de intensificación de tensiones en modo I [32]. DIC es una técnica óptica de no contacto que utiliza una (DIC-2D) o más cámaras (DIC-3D) para tener en cuenta el desplazamiento interno superficial, el desplazamiento y rotación como cuerpo rígido, y el desplazamiento fuera del plano; este último en caso de DIC-3D [20], [21].

Un sistema de medición DIC consta de una cámara con lente que adquiere las imágenes, una fuente de luz que da iluminación uniforme, una muestra pintada con fondo blanco y finos puntos negros para dar un alto contraste, un dispositivo que genere fuerzas conocidas como una máquina universal de ensayos, un computador con un software de correlación y un dispositivo de adquisición de datos que relacione la fuerza aplicada y la fotografía tomada en un tiempo t determinado [3], [33], [34]. Las cámaras deben estar montadas sobre un punto fijo y no se deben mover entre tomas [19], [35]. Una disposición de un montaje DIC típico se muestra en la Figura 1, en el cual se usan no una sino dos cámaras para adicionalmente realizar medidas de profundidad en cuerpos tridimensionales [33]. Se aprecia también una placa de calibración para estimar el tamaño de los objetos y su ubicación respecto al lente de la cámara. Estas placas de calibración no están disponibles para NCorr [4] y la calibración se hace de una forma diferente como se explica más adelante.

Figura 1: Ejemplo de montaje DIC.

Fuente: [33].

DIC es una técnica óptica que utiliza una (2D) [9], [18], [19] o dos o más (3D) [25], [33], [35] cámaras separadas por una distancia conocida, con el fin de tener en cuenta el movimiento de cuerpo rígido, la rotación y el desplazamiento perpendicular al lente, que aprovecha el cambio de intensidad de grises en fotografías secuenciales tomadas en una muestra antes y después de la deformación.

(1)

donde f(x, y) y g(x', y') representan los niveles grises de referencia antes y después de la deformación; (x, y) y (x', y') son las coordenadas de un punto en el subconjunto antes y después de la deformación; fm y gm son los valores de intensidad media de los subconjuntos de referencia y objetivo. La coordenada (x', y') que es la medida después de la deformación, se relaciona con la coordenada (x, y) que es la medida antes de la deformación, usando las ecuaciones mostradas en Ecuación (2) e ilustradas en la Figura 2.

Figura 2: Ejemplo de un subconjunto de una imagen antes y después de la deformación.

Fuente: adaptada de [33].

Las fotografías se digitalizan como mapas de los bits f(x, y) que permiten comparar la intensidad del gris antes y después de la deformación para obtener campos de desplazamiento utilizando la minimización de un criterio de correlación de bits [18], [35] como el descrito en la Ecuación (1). Los desplazamientos en la imagen deformada se pueden expresar usando expansiones de Taylor [3] como se muestra en la Ecuación (2), en donde sólo se muestran los términos de primer orden.

       (2)

Otro criterio de correlación bastante común es la suma cuadrática de la diferencia de cuadrados, SSD, como se muestra en la ecuación (3).

   (3)

No obstante, Sutton [1] advierte que, aunque el SSD es el menos influenciado por los criterios de optimización de la variación de la luz, también es el método más computacionalmente costoso. Sin embargo, con la amplia disponibilidad de potencia de cómputo actual, esto puede tener un efecto marginal en la obtención de resultados.

Una vez establecidos los desplazamientos ortogonales, las deformaciones unitarias, ε, se calculan usando relaciones de desplazamientos de Lagrange de la teoría de elasticidad [36] como se muestra en la Ecuación 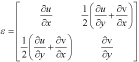(4).

                    (4)

Más aun, mediante el uso de relaciones elásticas [36], las tensiones, σ, se pueden calcular con la Ecuación (5).

         (5)

en donde E es el módulo elástico y ν es el módulo de Poisson.

La técnica DIC proporciona valores independientes de desplazamiento u y v en las direcciones X y Y, por lo que no es necesario el procesamiento posterior para usar datos. Si se usan dos o más cámaras, se pueden obtener mediciones estéreo como se muestra en [21], en donde se describen mediciones del campo w en el eje Z perpendicular al plano de los lentes. DIC es una técnica óptica sin contacto. La técnica se puede usar para medir muestras grandes o pequeñas, eventos estáticos o dinámicos y materiales rígidos o blandos. Los puntos se pueden agregar con un chorro de tinta, se pueden grabar o estampar [33].

De otro lado, la deformación unitaria en dirección paralela la carga P se puede calcular [36] como muestra la ecuación (6).

                                          (6)

Más allá aún, el problema de una placa con una perforación circular [36] de radio a y cargada remotamente por un esfuerzo uniforme uniaxial fue resuelto por Kirsh en 1898 [37], cuya notación se muestra en la Figura 3. El campo completo de tensiones, propuesto por Kirsh, viene dado por la Ecuación (7) [36].

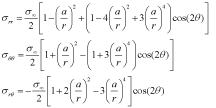(7)

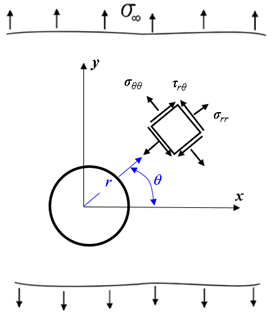
Figura 3: Notación de tensiones alrededor de una placa con una perforación circular.

Fuente: Elaboración propia.

Se aprecia en la Ecuación (8) que cuando r tiende a infinito la tensión tangencial σθθ, a θ=0º y 180º tiene a la tensión remota σoo, pero a compresión mientras que para ±90º σθθ alcanza un máximo de 3σoo a tensión. La tensión cortante y la tensión radial son nulas alrededor de la perforación pues el hueco es una superficie libre. Se aprecia también que si la placa es suficientemente grande, los componentes de tensión en el agujero son independientes del tamaño del agujero en sí..

Finalmente, Inglis [38] amplió el problema de Kirsch para una perforación elíptica de ancho a y altura b. El concentrador de esfuerzo, Kt, viene dada por la ecuación (8).

                                      (8)

Para un círculo, el ancho a es igual a la altura b entregando un Kt igual a 3. Entonces, el tener una solución analítica para el problema de una placa circular sometida a tracción unixaial remota se hace ideal para calibrar una técnica experimental.

a) Preparación y pruebas

La preparación de las probetas es tal vez la parte más importante en un desarrollo experimental [35]. Para DIC, la preparación de muestras consta en la aplicación de una capa de pintura blanca seguida de la aplicación de un punteado aleatorio de color negro como se muestra en la

Figura 1 .

Primeramente, se aplicó una capa blanca a la probeta. Seguidamente, y una vez seca la capa blanca, se procedió a agregar puntos negros aleatorios. Estos puntos se aplicaron de varias formas: usando aerosol negro

Figura 1 b, esparciendo puntos aleatorios con un pincel

Figura 1 c y con un marcador negro

Figura 1 d El fin de estos puntos es crear un patrón aleatorio que luego permita identificar los desplazamientos mediante el cambio de intensidad de grises de un malla arbitraria en el proceso de correlación.

Figura 1 . Ejemplo de preparación. a) capa blanca sobre la probeta #1 b) aplicación de punteado negro con spray c) aplicación de punteado negro con cepillo, d) punteado aleatorio en placa de drywall.

Fuente: Elaboración propia.

En diferentes fuentes [1], [33] recomienda usar un tamaño de punto de tal forma que se obtengan al menos 3 puntos negros en cada ventana de correlación, tal y como se muestra en la Figura 2 en donde a la izquierda se ve la muestra #1 y la localización de la ventana de correlación de la derecha.

Figura 2 . Ejemplo de distribución de puntos y de ventanas en NCorr.

Fuente: Elaboración propia.

Finalmente, la frecuencia de la fuente de luz debe ser acorde con el tiempo mínimo de exposición de la cámara, siendo la iluminación comercial la que necesita más tiempo y la luz estroboscópica la que requiere menos. El manual de usuario de 3D-VIC3 recomienda mantener el movimiento externo por debajo de 0.02 píxeles, por lo tanto, la frecuencia de la luz debe elegirse de acuerdo con la tasa de adquisición de cuadros [3]. En este caso se usó una fuente de luz fluorescente comercial blanca que es la que entrega menos interferencia con el contraste dado. Se tuvo bastante cuidado al operar el disparador e introducir movimiento de cuerpo rígido en las mediciones.

b) Las probetas

La primera probeta utilizada fue una probeta de policarbonato cortada por ASTM D638-I [39]. La segunda fue una placa plana de MDF. La tercera probeta fue igual a la #2 pero con una perforación en el centro para generar un concentrador de esfuerzos, estilo ASTM D5766 [40]. La cuarta probeta fue un bloque de madera para realizar pruebas de compresión. Finalmente, la quinta fue una placa plana de policarbonato con un hueco en el centro estilo ASTM D5766 [40]. Finalmente, una sexta probeta fue una placa plana de drywall, la cual no pudo ser sometida a tensión debido a su fragilidad no permitió los esfuerzos compresivos inducidos por las mordazas de agarre. Detalles de las muestras con diferentes patrones aleatorios se muestran en la Figura 3 y un resumen de las muestras usadas se hallan en la Tabla 1 .

Figura 3 . Probetas usadas en pruebas: a) Probeta #1 policarbonato, b) Probeta # 2, placa plana MDF, c) Probeta #3 placa plana MDF con concentrador de esfuerzos, d) Probeta # 4 bloque de madera para ensayo de compresión

Fuente: Elaboración propia.

Tabla 1 : Descripción de muestras usadas.

Fuente: Elaboración propia.

El punteado aleatorio de la Figura 3 se logró al variar tanto la cercanía de los puntos como su circularidad. Vale la pena aclarar que el desproporcionado punto negro observado en la esquina superior izquierda de la Figura 3 a no se tuvo en cuenta dentro de ninguna ventana de correlación en el área de análisis usada para esta muestra.

c) Equipos usados

Todos los ensayos fueron hechos en una maquina universal de ensayos Shimadzu AG-250 i con capacidad de carga de 250 kN y una celda de carga con capacidad de 1000 N, como se aprecia en la Figura 4, en donde observa un fondo negro colocado para aumentar el contraste al disminuir la reflexión de luz en la parte trasera de la probeta y al lente de la cámara. Los ensayos fueron realizados a una velocidad de carga de 0.5 mm/min. Sin embargo, para tener una referencia estable y minimizar una posible pérdida de foco, la aplicación de carga fue pausada al momento de tomar las fotografías. Esto también se hizo con el fin de documentar la carga aplicada al momento de tomar la fotografía. La adquisición de datos y control de la maquina fue hecha por medio del software Trapezium 2.23 (Shimadzu Coporation).

Con el fin establecer la utilización de cámaras comerciales para la técnica, se usaron diferentes cámaras con diferentes resoluciones e sensores. Todos los sensores son CCD (charged couple device). Los lentes utilizados en cada probeta son mostrados en la Tabla 2 así como la resolución de los sensores.

Figura 4 . Ejemplo de montaje de la probeta #5 en la maquina universal de ensayos.

Fuente: Elaboración propia.

Las cámaras fueron montadas sobre trípode para estabilizar la imagen y disminuir el movimiento de cuerpo rígido entre fotografías. La calibración de pixels a distancia se hizo por medio de la librería de NCorr en la que se le asigna una dimensión a una línea de la fotografía de referencia. Adicionalmente, la Figura 4 muestra el sistema de referencia usado. El eje Y es paralelo a la dirección de aplicación de la carga, mientras que el eje X es perpendicular a este y los dos ejes están en un plano paralelo al plano focal de la cámara.

Tabla 2 : Descripción de lentes y sensores CCD usados.

Fuente: Elaboración propia.

Finalmente, el código de NCorr corrió en un computador Intel ® con un procesador i7 a 3,4 GHz, 8MB de memoria RAM y una GPU Nvidia ®. Se puede usar un equipo con menor memoria RAM, pero el tiempo de correlación se afectaría significativamente.

Siguiendo el principio de funcionamiento de la técnica, se tomaron fotografías para cada probeta montada en la máquina universal y en un estado con carga cero que fueron usadas como estado de referencia. Adicionalmente, se tomó una segunda fotografía igualmente con carga cero para verificar la correlación. En todos los casos, se verificaron desplazamientos nulos en el plano entre las dos fotografías con carga cero, lo que indicó que la correlación y por ende medición son válidas. Todas las pruebas fueron sometidas a cargas en el régimen elástico y todas las pruebas fueron de carácter no destructivo.

a) Placa plana de policarbonato en tensión

Figura 5 : Resultado deformación unitaria  ɛ_yy para la probeta #1.

Fuente: Elaboración propia.

La prueba de tensión con la probeta # 1 (Figura 3 a) se realizó  con la cámara Cannon power Shot SX, como se describe en la Tabla 2 . Se obtuvieron los resultados deformación unitaria mostrados en la Figura 5 para un área de inspección de aproximadamente 25 mm de altura.

A pesar de la baja resolución de los resultados y de la escasa área de visión, se observó que tanto los desplazamientos u, y por lo tanto la deformación unitaria ɛ_xx (en la dirección perpendicular a la carga) son casi nulos como lo es esperado para esa combinación de geometría/carga/material. De otro lado, se aprecia como la deformación unitaria, ɛ_yy, en dirección paralela a la carga va aumentando a medida que la posición Y aumenta desde el apoyo fijo en la parte inferior. Por lo tanto en este caso, y con E de 2700 MPa para el policarbonato, se tiene una deformación unitaria máxima ɛ_yy estimada de 0.265 mm/mm, que no es muy cercana a la máxima observada en la Figura 5 . La diferencia se puede atribuir a la baja resolución dada por el lente que no permite capturar detalles.

b) Placa plana de MDF en tensión

La Figura 6 muestra los resultados de deformación unitaria paralela a la dirección de aplicación de la carga obtenidos de un ensayo de tensión para la probeta numero 2 usando la Canon power shot SX 210.

Figura 6 : Resultado de ɛ_yy, deformación unitaria en y para la probeta #2 con Canon power shot SX 210.

Fuente: Elaboración propia.

Al igual que en la probeta #1, se aprecian resultados similares en las direcciones perpendicular y paralelo a la carga. En este caso, el área de inspección usada es mayor y el módulo de elasticidad es diferente. Adicionalmente para la probeta número 2 se tomaron imágenes con la cámara de un teléfono móvil Huawei Mate20 lite. Se buscaba con esto comprobar que se podían obtener tomas más nítidas ya que al poseer activación del obturador por voz se tendría menos incidencia del movimiento de cuerpo rígido. Sin embargo, los campos hallados no mejoraron y tienen menos resolución. Por lo tanto, no se muestran los resultados ya que no se obtuvo una buena correlación.

c) Placa plana de MDF con concentrador de esfuerzos en tensión

La Figura 7 muestra las imágenes de los campos de desplazamiento y deformación unitaria del ensayo de la probeta número 3, la cual se sometió de igual manera a cargas de tensión. Las fotografías fueron tomadas con la cámara Cannon power Shot SX.

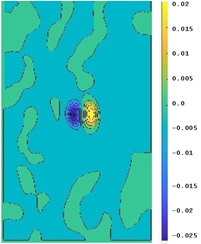
Figura 7 : Resultado para la probeta #3, a) u, desplazamiento en x, b) v, desplazamiento en y, c) ɛ_xx, deformación unitaria en x d) ɛ_yy, deformación unitaria en y.

Fuente: Elaboración propia.

A pesar de no tener una buena resolución para observar y cuantificar mayores detalles, se aprecia el gradiente de deformación unitaria producido por el concentrador de esfuerzos. Probablemente y por la falta de resolución del lente, no se puede llegar al nivel de detalle requerido para los desplazamientos presentes. También se aprecia como la perforación no es claramente diferenciada del material sólido.

Con el fin de analizar los resultados de las mediciones se realizó una simulación por elementos finitos de la probeta #3. El modelamiento numérico se realizó en SolidWorks Simulation ® usando una reducción 2D asumiendo esfuerzo plano y el Solver Direct Sparse. El modelo usó 1565 elementos cuadrangulares planos con 4 puntos jacobianos y 3135 nodos. Se usó un tamaño promedio de elemento de 2.5 mm con un refinamiento de 0.5 mm alrededor de la perforación circular. La Figura 8 a muestra los resultados de deformación unitaria, ɛ_yy, en dirección paralela a la carga. Se aprecia claramente las deformaciones más elevadas a 90º del punto de aplicación de la carga y menores en la dirección paralela a la carga tal como lo predice el modelo de Kirsch. De otro lado, la Figura 8 b muestra los resultados deformación unitaria, ɛ_xx, en dirección perpendicular a la carga, se aprecia cómo se presentan valores máximos espaciados en 90º comenzando a 45º del eje de aplicación de la carga mientras que se presentan deformaciones unitarias de signos opuestos en la dirección de la carga.

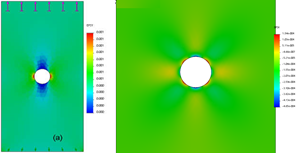
Figura 8 . Resultados de simulación por FEM para la probeta #3 a) ɛ_yy, deformación unitaria vertical, b) ɛ_xx, deformación unitaria horizontal.

Fuente: Elaboración propia.

d) Bloque de madera en compresión

Los resultados del ensayo realizado a la probeta #4, bloque de madera en compresión en sentido paralelo a las fibras, para poder apreciar las diferencias entre los resultados diferentes tipos de cargas, arrojando resultados bastante ruidosos. Se explican estos por el tamaño de la muestra que produjo deformaciones pequeñas para la resolución del lente usado, cámara Cannon power Shot SX. Por esta razón, no se presentan los resultados.

e) Placa plana de policarbonato en tensión

Finalmente, se muestran resultados tomados con el lente CANON macro EF 1:28, 100 mm para la probeta #5, placa plana de policarbonato en tensión con concentrador de esfuerzos. Se aprecia en la Figura 9 a la distribución del campo de deformación  unitaria en la dirección perpendicular a la carga, ɛ_xx, mientras que en la Figura 9 b muestra la distribución del campo de deformación unitaria en la dirección paralela a la carga, ɛ_yy.

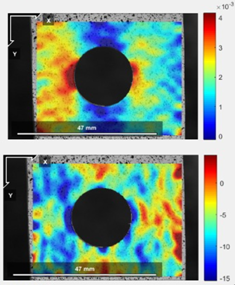
Figura 9. Campos de deformación unitaria para la probeta #5, a) ɛ_xx, perpendicular a la carga d), paralela a la carga ɛ_yy.

Fuente: Elaboración propia.

A pesar que la probeta #5 esta hecha de policarbonato y la probeta #3 está hecha de MDF, las dos tienen el mismo concentrador de esfuerzos y como los esfuerzos a que se sometieron están en el rango elástico, las formas de los campos de deformación unitaria sólo dependen de la tensión remota, σ_oo, como se muestra en la Ecuación (8). Esto es cierto para ɛ_yy, Figura 9 b, en donde se aprecia que las deformaciones unitarias en la dirección paralela a la carga son menores que las ubicadas 90º de estas. De otro lado, para ɛ_xx, Figura 9 a, se aprecian valores en promedio de un orden menor que ɛ_yy, como se mostró en la simulación por FEM de la Figura 8 . Sin embargo, como se discute en [21], los valores de desplazamiento en los bordes pueden tener un error inherente a la técnica. DIC busca el nivel de gris promedio de una región de interés sin deformar en una fotografía deformada, comenzando con las regiones adyacentes. Cuando hay fisuras esta región de interés deformada puede estar localizada en el lado opuesto de la grieta lo que entregaría deformaciones unitarias irreales [11]. En el caso de concentradores de esfuerzos, una región de interés puede o no encontrar dicha correlación al tener “vacío” en el lado del agujero, lo que hace que los resultados en los bordes tengan que ser analizados cuidadosamente. Por lo tanto, para, los valores arrojados por NCorr para ɛ_xx no corresponden exactamente a la solución teórica, Ecuación (8). La diferencia se atribuye a errores de correlación junto con falta de acercamiento del lente para poder observar los desplazamientos dentro del rango de los exhibidos en esta dirección.

De otro lado, al comparar los campos de deformación unitaria de la Figura 8 a (simulación por FEM) y de la Figura 9 a se aprecia la similitud.

Se evidenció que la medición de desplazamientos y sus campos de deformaciones asociados por medio de la técnica de correlación de imágenes digitales (DIC) es fuertemente dependiente de la magnificación óptica del lente usado y del tamaño promedio de los puntos aleatorios usados [5], [16]. Por lo tanto, se debe tener en cuenta la preparación el tamaño de los puntos sea acorde a la magnificación óptica disponible. Para bajos acercamientos ópticos, especialmente a distancias focales lejanas, las mediciones pueden usarse de manera descriptiva, p. ej. enseñanza y demostraciones, más de forma cuantitativa. De otro lado, se verificó que para mediciones cuantitativas se requiere de lentes con magnificación óptica apreciable a distancias focales cortas. Con esto en mente, se presentaron resultados de mediciones que muestran distribuciones de deformación unitaria de acuerdo a lo descrito por modelos teóricos que pueden ser usadas para validar simulaciones numéricas.

Se presentó y verificó un método para comprobar la correlación al comparar dos fotografías con carga cero. Se verificaron desplazamientos nulos entre dos fotografías subsecuentes con carga cero, lo que indica que la correlación y por ende medición realizada es válida. Esto es particularmente importante ya que valida el uso de los parámetros escogidos durante la correlación.

De la forma como se ha presentado y probado la técnica, se puede usar de manera descriptiva y con el cuidado adecuado, de forma cuantitativa en prácticas de laboratorio. Se resalta que con el uso de software libre el costo de implementación de la técnica, para el fin citado, es ostensiblemente menor que una opción comercial. Sin embargo, se pueden tener limitaciones debido a la falta de un método de calibración con una incerteza menos dependiente de la subjetividad del operario, tal y como lo hace Ncorr.

Adrián Eduardo Peñaranda Domínguez e Iván Mauricio Castillo González agradecen el apoyo financiero dado por la USTA Bucaramanga por medio de la VI convocatoria para semilleros de investigación, así como a los prof. Félix A. Pérez, Leonardo Monroy y Emerson Olaya quienes colaboraron en algunos ensayos y gestión de compras. Jorge G. Díaz agradece especialmente al Dr. Camilo Villabona por facilitar la cámara Cannon macro EF.

[1]   M. A. Sutton, J. J. Orteu, and H. Schreier, Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications. Boston: Springer, 2009.

[2]   W. H. Peters and W. F. Ranson, “Digital Imaging Techniques In Experimental Stress Analysis,” Opt. Eng., vol. 21, no. 3, 1982, doi:10.1117/12.7972925.

[3]   E. M. C. Jones and M. . Iadicola, “A Good Practices Guide for Digital Image Correlation,” iDIC. iDIC Society, p. 101, 08-Oct-2018.

[4]   J. Blaber, A. Adair, and A. Antoniou, “Ncorr: Open-Source 2D Digital Image Correlation Matlab Software,” Exp. Mech., vol. 55, no. 6, pp. 1105–1122, 2015, doi:10.1007/s11340-015-0009-1.

[5]   S. H. Ju, S. H. Liu, and K. W. Liu, “Measurement of stress intensity factors by digital camera,” Int. J. Solids Struct., vol. 43, no. 5, pp. 1009–1022, 2006, doi:10.1016/j.ijsolstr.2005.05.052.

[6]   V. Belloni, R. Ravanelli, A. Nascetti, M. Di Rita, D. Mattei, and M. Crespi, “py2DIC: A New Free and Open Source Software for Displacement and Strain Measurements in the Field of Experimental Mechanics,” Sensors, vol. 19, no. 18, p. 3832, Sep. 2019, doi:10.3390/s19183832.

[7]   E. Tudisco, E. Andò, R. Cailletaud, and S. A. Hall, “TomoWarp2: A local digital volume correlation code,” SoftwareX, vol. 6, pp. 267–270, 2017, doi:10.1016/j.softx.2017.10.002.

[8]   B. Dong, F. Zeng, and B. Pan, “A Simple and Practical Single-Camera Stereo-Digital Image Correlation Using a Color Camera and X-Cube Prism,” Sensors, vol. 19, no. 21, p. 4726, Oct. 2019, doi:10.3390/s19214726.

[9]   R. Harilal and M. Ramhi, “Adaptation of Open Source 2D DIC Software Ncorr for Solid Mechanics Applications,” in 9th International Symposium on Advanced Science and Technology in Experimental Mechanics, 2014.

[10] C. H. Valencia Niño and S. N. Cáceres Quijano, “Modelo de optimización en la gestión de inventarios mediante algoritmos genéticos,” ITECKNE, vol. 8, no. 2, pp. 156–162, Dec. 2011, doi:10.15332/iteckne.v8i2.34.

[11] G. L. G. Gonzáles, J. G. Diaz, J. A. O. González, J. T. P. Castro, and J. L. de F. Freire, “Determining SIF using DIC considering Crack closure and blunting,” in Experimental and Applied Mechanics. Vol 4., vol. 4, A. T. Zehnder, Ed. Orlando, FL: Springer, 2017, pp. 25–36.

[12] G. N. Eichhorn, A. Bowman, S. K. Haigh, and S. Stanier, “Low‐cost digital image correlation and strain measurement for geotechnical applications,” Strain, Apr. 2020, doi:10.1111/str.12348.

[13] J. Cui, S. Wang, S. Wang, G. Li, P. Wang, and C. Liang, “The Effects of Strain Rates on Mechanical Properties and Failure Behavior of Long Glass Fiber Reinforced Thermoplastic Composites,” Polymers (Basel)., vol. 11, no. 12, p. 2019, Dec. 2019, doi:10.3390/polym11122019.

[14] T. A. Dutra, R. T. L. Ferreira, H. B. Resende, and A. Guimarães, “Mechanical characterization and asymptotic homogenization of 3D-printed continuous carbon fiber-reinforced thermoplastic,” J. Brazilian Soc. Mech. Sci. Eng., vol. 41, no. 3, p. 133, Mar. 2019, doi:10.1007/s40430-019-1630-1.

[15] A. N. Dickson and D. P. Dowling, “Enhancing the bearing strength of woven carbon fibre thermoplastic composites through additive manufacturing,” Compos. Struct., vol. 212, pp. 381–388, Mar. 2019, doi:10.1016/j.compstruct.2019.01.050.

[16] S. N. Omkar, G. B. Praveen, and A. Singh, “Investigation of Wrist Extension Using Three Dimensional Digital Image Correlation,” Biomed. Biotechnol., vol. 1, no. 1, pp. 1–7, 2013, doi:10.12691/bb-1-1-1.

[17] J. P. M. Hoefnagels, M. P. F. H. L. van Maris, and T. Vermeij, “One-step deposition of nano-to-micron-scalable, high-quality digital image correlation patterns for high-strain in-situ multi-microscopy testing,” Strain, vol. 55, no. 6, p. e12330, Dec. 2019, doi:10.1111/str.12330.

[18] R. Zhang and L. He, “Measurement of mixed-mode stress intensity factors using digital image correlation method,” Opt. Lasers Eng., vol. 50, no. 7, pp. 1001–1007, 2012, doi:10.1016/j.optlaseng.2012.01.009.

[19] J. G. Díaz Rodríguez, G. Gonzales, J. A. Ortiz Gonzalez, and  de F. F. José Luiz, “Analysis of Mixed-mode Stress Intensity Factors using Digital Image Correlation Displacement Fields,” in Procceedings of the 24th ABCM International Congress of Mechanical Engineering, 2017.

[20] M. Vormwald, Y. Hos, J. L. F. Freire, G. L. G. Gonzáles, and J. G. Díaz, “Crack tip displacement fields measured by digital image correlation for evaluating variable mode-mixity during fatigue crack growth,” Int. J. Fatigue, vol. 115, no. 1, pp. 53–66, Oct. 2018, doi:10.1016/j.ijfatigue.2018.04.030.

[21] M. Vormwald, Y. Hos, J. L. F. Freire, G. L. G. Gonzáles, and J. G. Díaz, “Variable mode-mixity during fatigue cycles – crack tip parameters determined from displacement fields measured by digital image correlation,” Frat. ed Integrità Strutt., vol. 11, no. 41, pp. 314–322, Jun. 2017, doi:10.3221/IGF-ESIS.41.42.

[22] M. Mokhtarishirazabad, P. Lopez-Crespo, B. Moreno, A. Lopez-Moreno, and M. Zanganeh, “Evaluation of crack-tip fields from DIC data: A parametric study,” Int. J. Fatigue, vol. 89, pp. 11–19, 2016, doi:10.1016/j.ijfatigue.2016.03.006.

[23] C. H. Wolf, S. Henkel, A. Burgold, Y. Qiu, M. Kuna, and H. Biermann, “Investigation of fatigue crack growth under in-phase loading as well as phase-shifted loading using cruciform specimens,” Int. J. Fatigue, vol. 124, pp. 595–617, Jul. 2019, doi:10.1016/j.ijfatigue.2019.03.011.

[24] A. Kotousov, P. Lazzarin, F. Berto, and L. P. Pook, “Three-dimensional stress states at crack tip induced by shear and anti-plane loading,” Eng. Fract. Mech., vol. 108, pp. 65–74, 2013, doi:10.1016/j.engfracmech.2013.04.010.

[25] M. R. Molteno and T. H. Becker, “Mode I – III Decomposition of the J -integral from DIC Displacement Data,” Strain, vol. 51, no. 6, pp. 492–503, 2015, doi:10.1111/str.12166.M.

[26] G. L. G. Gonzáles, J. A. O. González, J. T. P. de Castro, and J. L. de F. Freire, “Measuring elastoplastic strain loops in the near crack-tip region using a Stereo Microscope DIC system,” Int. J. Fatigue, vol. 133, p. 105427, Apr. 2020, doi:10.1016/j.ijfatigue.2019.105427.

[27] H. Al-Salih, M. Juno, W. Collins, C. Bennett, J. Li, and E. J. Sutley, “Evaluation of a Digital Image Correlation Bridge Inspection Methodology on Complex Distortion-Induced Fatigue Cracking,” Procedia Struct. Integr., vol. 17, pp. 682–689, 2019, doi:10.1016/j.prostr.2019.08.091.

[28] J. G. Diaz and D. C. Paez, “Identification of Crack Tip Location using Edge Detec-tion Algorithms and Artificially Generated Displace-ment Fields,” in LNEE, vol. 658, D. Cortes, V. Hoang, and T. Dan, Eds. Bogota: Springer, 2020, pp. 1–8.

[29] A. D. Pertuz-Comas, O. A. Gonzalez-Estrada, and C. Graciano, “Investigación en ingeniería en Colombia,” Rev. UIS Ing., vol. 19, no. 1, pp. 1–3, 2020, doi:10.18273/revuin.v18n4-2020021.

[30] M. A. Sutton, W. J. Wolters, W. H. Peters, W. F. Ranson, and S. R. McNeill, “Determination of Displacements using an Improved Digital Correlation Method,” Image Vis. Comput., vol. 1, no. 3, pp. 133–139, 1983, doi:10.1016/0262-8856(83)90064-1.

[31] W. H. Peters, F. Ranson, W, M. A. Sutton, T. C. Chu, and J. J. Anderson, “Application Of Digital Correlation Methods To Rigid Body Mechanics,” Opt. Eng., vol. 22, no. 6, 1983, doi:10.1117/12.7973231.

[32] S. R. McNeill, W. H. Peters, and M. A. Sutton, “Estimation of Stress Intensity Factor by Digital Image Correlation,” Eng. Fract. Mech., vol. 28, no. 1, pp. 101–112, 1987, doi:10.1016/0013-7944(87)90124-X.

[33] L. D. Rodrigues, “Aplicação da técnica DIC a espécimes com diferentes formas , materiais e gradientes de deformação,” PUC Rio, 2014.

[34] L. C. S. Nunes, J. M. L. Reis, and H. S. da Costa Mattos, “Parameters identification of polymer concrete using a fracture mechanics test method and full-field measurements,” Eng. Fract. Mech., vol. 78, no. 17, pp. 2957–2965, Dec. 2011, doi:10.1016/j.engfracmech.2011.08.013.

[35] J. G. Diaz Rodriguez, “Linear elastic fracture mechanics analysis of fatigue crack growth under complex loading using the Digital Image Correlation technique,” Pontifícia Universidade Católica do Rio de Janeiro, Rio de Janeiro, Brazil, 2018.

[36] M. H. Sadd, Elasticity, 3rd ed. Kingston, Rhode Island: Elsevier, 2014.

[37] E. G. Kirsch, “Die Theorie der Elastizität und die Bedürfnisse der Festigkeitslehre,” Zeitschrift des Vereines Dtsch. Ingenieure, vol. 42, pp. 797–807, 1898.

[38] C. Inglis, “Stresses in Plates Due to the Presence of Cracks and Sharp Corners,” Trans. Inst. Nav. Archit., vol. 55, pp. 219–241, 1913.

[39] ASTM, ASTM D638. Standard Test Method for Tensile Properties of Plastics. USA: American society of testing materials, 2014.

[40] ASTM, ASTM D5766. Standard Test Method for Open-Hole Tensile Strength of Polymer Matrix Composite Laminates. USA, 2018.