http://dx.doi.org/10.15649/2346030X.2470
Modelos logísticos estocásticos: una revisión de la literatura.
Stochastic logistic models: a literature review.
Javier Martínez-Bernal1
Ricardo Andrés Cuervo-Cruz2
Javier Arturo Orjuela-Castro3
-
Universidad Distrital Francisco José de Caldas – Colombia. E-mail: jmartinezb@correo.udistrital.edu.co Autor de correspondencia
- Universidad Francisco de Paula Santander – Colombia.
Recibido: 19 de septiembre de 2020.
Aprobado: 11 de noviembre de 2020.
Resumen—El presente artículo se realiza con el objetivo de establecer el estado del arte de los modelos de localización, inventario y ruteo con parámetros estocásticos. Se realizó una revisión sistemática de la literatura en las bases de datos ScienceDirect, ScholarGoogle, SpringerLink, Scopus, SemanticScholar, Scielo y ResearchGate. A través de preguntas orientadoras, se seleccionaron 99 artículos, de los cuales el 74% es literatura reciente entre 2015 y 2019. Se clasificaron los modelos individuales logísticos estocásticos, se propuso una taxonomía con un enfoque de investigación de operaciones, a partir de sus características, parámetros, restricciones, funciones objetivo y métodos de solución utilizados. Asimismo, se identificaron las tendencias y las futuras líneas de investigación. Como conclusión se identifican nuevas estrategias y políticas operativas que permiten mejorar el desempeño de la cadena de suministro, igualmente la ausencia de métodos de solución eficientes ha sido evidente en grandes instancias, según la vida real.
Palabras clave: Estocasticos; Modelos de inventario; Localizacion; Instalaciones; Multieslabon; Modelos de ruteo estocastico.
Abstract—The present article is done with the aim of to establish the state of the art of location, inventory and routing models with stochastic parameters. The literature reviewed was classified with an operations research approach. A systematic review of the literature in the databases ScienceDirect, ScholarGoogle, SpringerLink, Scopus, SemanticScholar, Scielo, and ResearchGate was done. Through guiding questions, 99 articles were selected, of which 74% is recent literature between 2015 and 2019. Stochastic logistic individual models were classified, a taxonomy with an operations research approach was proposed, from their characteristics, parameters, restrictions, the objective functions and solution methods used. Also, the trends and the future lines of research were identified. As a conclusion new strategies and operating policies that permit improve supply chain performance are identified, also the absence of efficient solution methods has been evident to large instances, according to real-life.
Keywords: Stochastics; Inventory models; Location; Facilities; Multi-echelon; Vehicle Routing Problem; Stochastic models.
Los modelos logísticos deben adaptarse a situaciones y negocios, la transformación de un modelo determinista mediante la adición de parámetros estocásticos representa mejor una situación de la vida real [1], la inclusión de aleatoriedad genera mayor complejidad [2]. Se han realizado varias revisiones de la literatura enfocados a modelos deterministicos. A nivel de inventarios, [3] y [4] realizan una revisión de los problemas de inventario multieslabón, [5] y [6] realizan una revisión exhaustiva de los problemas de localización de instalaciones; En cuanto al ruteo estocástico; [7] y [8] revisan la literatura y presentan una tipología de los trabajos publicados en un periodo de 10 años.
El propósito principal de esta investigación es establecer, a partir de una revisión de la literatura, una taxonomía en donde se clasifican investigaciones recientes en el modelado estocástico en logística con el fin de establecer el estado del arte de estudios que brinden una mejor aproximación entre el modelo y lo real. Los modelos que hacen parte de la revisión se limitan a los de localización, inventario y ruteo por separado. Se identifica, a la luz de los expertos en este campo, vacíos del conocimiento y líneas futuras de investigación.
Las operaciones logísticas impactan en el valor del producto final, desarrollar mejores modelos que amortiguen los efectos de la aleatoriedad, minimizando los costos representa un beneficio para todos los eslabones de la cadena desde el proveedor hasta el cliente.
El presente trabajo es resultado de una revisión sistemática de la literatura [9] que se desarrolla a través de la búsqueda, recolección y síntesis de información, tomada de artículos en revistas científicas mediante las bases de datos ScienceDirect, ScholarGoogle, SpringerLink, Scopus, SemanticScholar, Scielo y ResearchGate. Se plantearon tres conjuntos de palabras claves (ver la tabla 1). Las preguntas orientadoras de la búsqueda fueron: ¿Dónde se presenta la estocasticidad en cada modelo?, ¿Cómo han evolucionado a través de los años estos modelos?, ¿Cuáles son los temas prometedores que no se han estudiado en estos tres campos?
Tabla 1: Palabras clave usadas en la revisión.
MODELOS |
PALABRAS CLAVE |
Inventario |
Stochastics, Inventory models, Inventory system, Multi-echelon, Multilevel |
Localización |
Location, Stochastics models, Facilities, Ubication |
Ruteo |
Stochastic VRP, SVRP, Stochastic Vehicle Routing Problem |
Fuente: Elaboración propia.
Los artículos consultados corresponden a ScienceDirect y ScholarGoogle con el 27 y 24% del total respectivamente, SpringerLink y Scopus con un 22% y 21%, el 6% restante fueron encontrados en SemanticScholar, Scielo y ResearchGate. Para la selección se tuvo en cuenta documentos que correspondieran a los últimos 5 años, literatura reciente que aborda modelos estocásticos logísticos, al menos el 70% de los artículos seleccionados cumplen con este criterio, Figura 1.
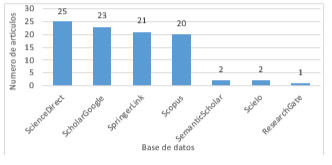
Figura 1: Distribución de los artículos por base de datos consultada.
Fuente: Elaboración propia.
El 61% de los artículos consultados comprenden el año 2017 y 2019 de publicación, se puede evidenciar que, aunque la mayoría de los artículos son recientes, se cuenta con artículos seminales sobre modelos logísticos estocásticos. La figura 2 muestra la distribución de los artículos por su fecha de publicación.

Figura 2: Distribución de los artículos según año de publicación.
Fuente: Elaboración propia.
El enfoque de investigación fue mixto (con análisis descriptivo e interpretativo), puesto que los modelos fueron caracterizados, a partir de las taxonomías se describe y resume los datos obtenidos mediante la frecuencia, moda y porcentajes. Adicionalmente, se establecen los tipos de modelo, variables, parámetros y restricciones más comunes en la literatura, se logró identificar la tendencia de las funciones objetivo y métodos de solución empleados además de los vacíos del conocimiento para cada uno de los modelos presentados.
En el presente capítulo se realiza la taxonomía y descripción de los modelos. Primero se presentan la gestión de inventarios para múltiples eslabones. Luego los modelos de localización con parámetros estocásticos. Se finaliza con los modelos de ruteo (SVRP, por sus siglas en inglés stochastic vehicle routing problem). Se destina un capítulo aparte para la función objetivo y los métodos de solución.
a. Inventarios
La gestión de inventarios determina cuándo realizar el pedido y su tamaño con el propósito de satisfacer al cliente y el nivel de inventario al menor costo [10], importante en empresas cuyo inventario representa el 50% o más de sus activos totales [3]. Las operaciones de logística y las decisiones relacionadas para asegurar el flujo de producto ininterrumpido y oportuno a través de diferentes segmentos de la CS, depende de las acciones sobre inventario [11] y la utilización de medios de transporte eficientes [12]. La administración de inventario multieslabon permite la coordinación del inventario a través de la CS mitigando el efecto látigo [3], [13]–[16]. Una incorrecta estimación de la demanda y la distorsión de la información desde los eslabones aguas abajo al extremo aguas arriba de la CS aumenta el efecto látigo y como consecuencia el costo global de la CS [12].
El primer modelo de inventario multieslabón con demanda estocástica fue presentado por Clark y Scraft, plantea una CS para dos eslabones, un proveedor con varios minoristas, con una política de inventarios de revisión periódica (s, S) que minimiza el costo total de la gestión de inventarios en la CS [17]. Este problema lo formulan con programación dinámica y se resuelve mediante una heurística basada en descomposición. Demuestran que el procedimiento propuesto por ellos se aleja de la optimalidad, aunque sí es un método válido para una solución inicial factible. En [18], amplían la investigación de Clark y Scraft para modelos cuyos horizontes de planeación son infinitos y con una demanda con distribución normal. Demostraron que los cálculos requeridos se simplifican y que una estructura con un proveedor y varios minoristas se aproxima a una estructura en serie bajo ciertas condiciones. En [19] presenta un modelo de inventarios para N eslabones con una estructura en serie, bajo el supuesto de que no hay costos de ordenar, extiende el modelo a un sistema de montaje donde los materiales fluyen en lotes. Generaliza los resultados de Clark y Scraft demostrando la optimalidad de la política (R, nQ) y ratifica que para los sistemas de distribución no existen políticas óptimas.
Los autores en [4] realizan una revisión de la literatura y destaca que en la práctica las políticas de inventario son muchas más que revisión continua y revisión periódica, planteando que futuras investigaciones deben considerar métodos existentes o nuevos para caracterizar dichas políticas, además de políticas de devolución de artículos defectuosos, por su parte [20] realiza una distinción entre los modelos de servicio garantizado y los de servicio estocástico, destacando las implicaciones de estos enfoques en los modelos. Más recientemente[21] realizan una tipología de modelos de inventario multieslabón estocásticos entre los años 1959 y 2016.
1. Modelos con plazos de entrega o demanda aleatorios y sus políticas
Para [22], existen 5 supuestos sobre los plazos de entrega (LT, por sus siglas en ingles lead time), su relevancia recae en la toma de decisiones según la perspectiva del LT. Algunos autores como [23], consideran incorrecto que los LT sea una variable aleatoria, independiente e idénticamente distribuida, dado que para que esto ocurra, la demanda debe ser no estacionaria y que el proveedor tenga inventario disponible. Por su parte [24], plantea que varios LT generan el cruce de órdenes (Order Crossover), este fenómeno ocurre por diferencias en los LT de las órdenes cuando no llegan en la misma secuencia en que fueron colocadas. El impacto de ello en el abastecimiento de uno o varios eslabones de la CS debe ser considerado en los modelos de inventario, [14] lo estudia para un eslabón. Recientemente [25], [26] y [27] abordan esta problemática en un solo eslabón, declarando la necesidad de extender el modelo a multi eslabón en futuras investigaciones.
Para modelar la demanda en los problemas de inventario estocásticos, se recomienda tener en cuenta su tamaño. Si la demanda es pequeña, se usa una distribución discreta y Poisson, si es grande se usa una distribución continua y de preferencia la Normal [28]. Algunos autores consideran que la distribución Normal es una opción con limitaciones, como la probabilidad de tomar valores negativos y un bajo coeficiente de variación, es mejor considerar distribuciones Log normal, Weibull o Gamma [29].
Las políticas de inventario utilizadas con mayor frecuencia en los modelos de inventario son: de revisión continua, empleadas cuando el horizonte de planeación es infinito, y de revisión periódica, para horizontes de planeación finito. En las políticas de revisión continua se encuentran: la política de pedidos por lotes (R, Q) para un solo eslabón, para varios eslabones están la política de pedido por lotes basada en stock y reemplazo 1 a 1 (s-1, s). En las políticas de revisión periódica, se usa la política de pedido variable (R, T) para un solo eslabón y políticas de intervalo fijo y pedido límite para varios eslabones [30]. Bajo el supuesto de demanda estocástica para modelos de varios eslabones, con el sistema (R, T) es más fácil coordinar la CS que con una política de revisión continua [31], [32], ya que el mismo ritmo de reordenamiento hace que sea fácil tomar las decisiones operativas de transporte y programación de rutas en cada centro de distribución (CD) y ahorrar costos [33], [34].
2. Taxonomía de los Modelos de Inventario en Cadenas de Suministro
En esta sección se presentan los artículos de inventario, cuyas decisiones son tomadas para dos o más eslabones de forma simultánea, la clasificación se dividió en cinco conjuntos, resumidos en tipos de modelos, métodos de solución en la tabla 2, variables de decisión y restricciones en la tabla 3 y, parámetros en la tabla 4.
2.1. Tipos de Modelos y Métodos de Solución
El modelo matemático más utilizado es la programación dinámica (PD), seguido de la programación no lineal entera mixta (PNLEM) y la programación no lineal (PNL). La programación entera (PE) y programación lineal entera mixta (PLEM) representan la menor proporción, figura 3.

Figura 3: Grafica de porcentajes según tipo de modelo.
Fuente: Elaboración propia.
En [35] modela una CS con punto de fabricación y un CD como un sistema de colas para determinar el costo total promedio, considera el tiempo de entrega estocástico y endógeno como una combinación de los tiempos de fabricación y transporte, emplea una HDF para su solución. Por su parte, [12] propone un modelo con cuatro eslabones para la reposición de inventarios, implementa una política ordenar-hasta (order-up-to), con múltiples puntos de reorden que dependen del método de transporte, demuestra que el método AAB tiene una mayor eficiencia y mejores cualidades de soluciones que el algoritmo evolutivo GA. Los resultados del enfoque propuesto son probados y validados en varios conjuntos de datos utilizando un GAP y un análisis ANOVA de dos vías.
El estudio de [36] presenta un modelo de revisión continua, en donde un CD realiza una política de asignación equilibrada a minoristas con base en quien reduce más los costos al momento de la asignación de la orden, emplean dos heurísticas, una Optimización recursiva y la heurística de descomposición-agregación. En [37] formulan un problema de programación dinámica para un servicio garantizado, consideran el efecto de las horas extras y la subcontratación, incluyen el stock de seguridad en dos eslabones, tienen en cuenta el tiempo de producción endógeno haciendo uso de la capacidad flexible, para manejar el exceso de demanda y optimizar los tiempos de producción.
El autor en [38] estudia dos modelos para optimizar el inventario multieslabón en una red de distribución con demandas y LT estocásticos. Compara el desempeño de un modelo de servicio garantizado (GSM) con un modelo de servicio estocástico (SSM), emplea una política (R, Q), incluye costos de pedido, mantenimiento y de flexibilidad. El GSM supera el SSM en más del 80% de los casos simulados y una mejora del costo total promedio en el 10%, mejora el costo con diferencia relativamente baja entre los dos enfoques. En [39] comparan tres políticas de inventario bajo una demanda estacional en una CS con dos eslabones, un almacén y N minoristas. El modelo lo soluciona con una metodología de dos fases, en la primera con demanda determinista y la segunda estocástica, la resuelve con múltiples escenarios. Desarrollan una heurística de dos fases para resolver el modelo [40].
En el estudio de [41] plantean un enfoque de optimización robusta con datos tratados mediante machine learning, proporciona un equilibrio flexible entre la robustez y el desempeño que responde a la falta de conocimiento respecto a la forma en que se distribuye la demanda en la práctica. En [42] proponen y evalúan una heurística de eslabón modificado con política (R, Q) de fácil implementación, no requiere de entero multiplicativo o sincronización para ordenar, demuestra que la política propuesta es asintótica al óptimo que supera a la heuristica eslabon-stock (R, Q).
Tabla 2: Inventario multieslabon, modelos y métodos de solución.
Referencia |
año |
Tipos de modelo |
Métodos de solución |
Función objetivo |
|||||||||||||||
PLEM |
PNL |
PNL-EM |
PD |
PE |
AG |
AAB |
S |
HBD |
HDF |
ABL |
ME |
PU |
HAB |
ADA |
Objetivo |
Único |
Múltiple |
||
[17] |
1960 |
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
MIN |
x |
|
[18] |
1984 |
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
MIN |
x |
|
[19] |
2000 |
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
MIN |
x |
|
[43] |
2017 |
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
MIN-MAX |
|
x |
[44] |
2017 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
MIN |
x |
|
[45] |
2017 |
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
MIN |
x |
|
[46] |
2017 |
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
MIN |
x |
|
[47] |
2017 |
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
MIN |
x |
|
[12] |
2017 |
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
MAX |
x |
|
[35] |
2017 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
MIN |
x |
|
[36] |
2017 |
|
x |
|
|
|
|
|
x |
x |
|
x |
|
|
|
|
MIN |
x |
|
[48] |
2018 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
MIN |
x |
|
[37] |
2018 |
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
MIN |
x |
|
[38] |
2018 |
|
|
x |
|
|
|
|
x |
|
|
x |
|
|
|
|
MIN |
x |
|
[39] |
2018 |
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
MIN |
x |
|
[49] |
2018 |
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
MIN |
x |
|
[41] |
2018 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
MIN |
|
x |
[42] |
2018 |
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
MIN |
x |
|
[50] |
2019 |
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
MIN |
x |
|
[51] |
2019 |
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
MAX |
x |
|
[52] |
2019 |
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
MIN |
x |
|
[40] |
2019 |
|
|
x |
|
|
x |
|
|
|
x |
x |
x |
|
|
|
MIN |
x |
|
Total |
2 |
4 |
6 |
8 |
2 |
1 |
1 |
3 |
5 |
6 |
4 |
3 |
1 |
1 |
2 |
|
20 |
2 |
|
Fuente: Elaboración propia.
Notación: PLEM: Programación Lineal Entera Mixta, PNL: Programación No lineal, PNLEM: Programación Entera mixta no lineal, PD: Programación dinámica, PE: Programación estocástica, AG: Algoritmo genético, AAB: Algoritmo de alimentación bacteriana, S: Simulación, HBD: Heurísticas basadas en descomposición, HDF: Heurística de dos fases basadas en descomposición, ABL: Algoritmo de búsqueda local, ME: Métodos exactos, PU: Punto interior, HAB: Heurística basada en algoritmos de búsqueda, ADA: Algoritmo desarrollado por el autor.
2.2. Clasificación por Variables de Decisión y Restricciones
Se definieron tres grupos para clasificar las variables de decisión: costos, cantidades y tiempo. Se identificaron 3 tipos de costos en las funciones objetivo, el beneficio como diferencia entre costo y precio de venta. Las restricciones se agrupan en diez tipos, ver la Tabla 3.
Los autores en [45] estudian las políticas de reabastecimiento multiproducto en un estructura típica de distribución con ajustes y variantes a las políticas (r, Q), Establece medidas de desempeño para comparar el desempeño de las políticas, encuentran que la política integrada (R, nQ) se comporta mejor respecto al costo total esperado. En [47] consideran un sistema de inventario con limitaciones de capacidad con horizonte de planeación finito e infinito. Para aquellas estructuras con cuello de botella en eslabones aguas abajo y utilización del sistema por encima de cierto umbral, encontraron la política óptima como una variación de order-up-to, demuestran que dependen del inventario aguas arriba.
El estudio realizado por [43] plantean un modelo para obtener el tamaño de lote y la cantidad a ordenar óptimos para productos imperfectos, maximizan el beneficio total de la CS y minimizan el costo del inventario, incluyen múltiples restricciones estocásticas que limitan los costos a un presupuesto asignado. En [49] estudian una CS con dos eslabones, cuyas decisiones de inventario son independientes, encuentran que los niveles de existencias de aguas abajo están influenciadas por la demanda, mientras que el inventario de aguas arriba está más influenciada por costos de inventario e incertidumbre del suministro, el costo de penalización minorista es marginal. En [52] estudian una política de revisión continua para múltiples productos en una CS de cuatro eslabones, con limitaciones de espacio para el stock de seguridad. Utilizan una heurística de búsqueda exhaustiva, determinan la política que optimiza el índice de rotación de inventario y el costo total, mientras se maximiza el nivel de servicio. Se modela la demanda aleatoria estacional y los plazos de entrega mediante una distribución normal. En la Figura 4 se muestra la relación entre las variables de decisión más empleadas.
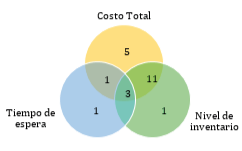
Figura 4: Frecuencia de uso de variables de decisión
Fuente: Elaboración propia.
2.3 Clasificación por Tipos de Parámetros
Para la clasificación por parámetros se agruparon en cuatro categorías: Inventario/producción, tiempos, costos, otros. En otros se listan 4 parámetros que le agregan valor al modelo de inventario multieslabón. Ver Tabla 4.
Los autores en [44] proponen un modelo sostenible de inventarios integrado VMI con consolidación de pedidos, costo de flete dependiente del volumen, demanda aleatoria y LT constantes, consideran dos medios de transporte para la distribución donde la relación entre el plazo de entrega-emisiones es inversamente proporcional, con una política (s-1, S), buscan minimizar el costo total y las emisiones de CO2. En [50] aplican el modelo de Stenius a un caso práctico de una empresa cuyo transporte de producto es costoso por las dimensiones del producto. En [48] presentan un modelo centralizado para tres eslabones de circuito cerrado (close loop (CLSC)), un fabricante, un reconstructor y un minorista. Se considera la demanda y la tasa de devolución de artículos defectuosos como parámetros aleatorios. Encontraron CLSC más rentable que una CS típica de fabricación-inventario, cuando el coste de fabricación del producto devuelto es significativamente más bajo en comparación con el coste de fabricación del nuevo producto.
Tabla 3: Taxonomía Inventarios, Variables de decisión y Restricciones
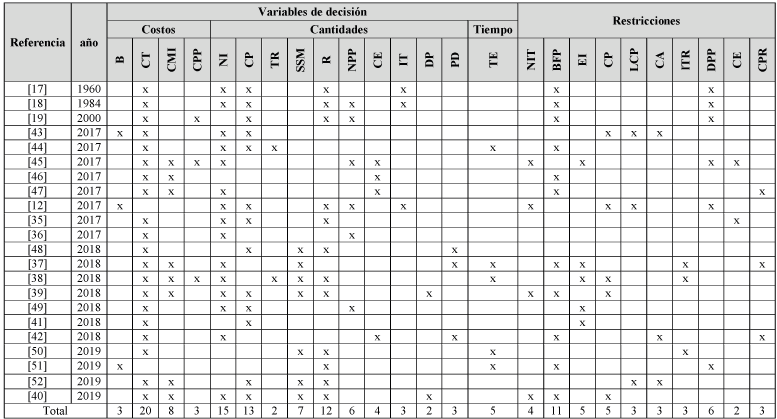
Fuente: Elaboración propia.
Variables de decisión: B: Beneficio, CT: Costo total, CMI: Costo de mantener inventario, CPP: Costo de pedido pendiente, NI: Nivel de inventario, CP: cantidad a pedir, TR: Tasa de reposición, SSE: Stock de seguridad del eslabón, R: Punto de reorden, NPP: Nivel de pedido pendiente, CE: Cantidad a enviar, IT: Inventario en tránsito, PD: Cantidad a producir, DP: demanda perdida, TE: Tiempo entre envíos, Restricciones: NIT: Nivel de inventario de la tienda, BFP: Balance de flujo de producto, EI: Equilibrio de inventario, CP: Cantidad de pedidos, LCP: Limites en la cantidad a pedir, CA: Capacidad del almacén, LTR: Limite en Tasa de reposición, DPP: Cumplimiento de Demanda con pedidos pendientes, CE: Cantidad del envió, CPR: Capacidad de producción.
En [51] proponen un modelo para coordinar una CS de dos niveles que emplea revisión periódica con demanda estocástica para un minorista con estrategias promocionales y ampliación del mercado. El minorista genera rentabilidad en la CS aguas arriba y disminuye el nivel de servicio de la CS, consideran un mecanismo de pagos a crédito teniendo en cuenta las tasas de retorno de inversión de cada eslabón.
Tabla 4: Taxonomía Inventarios, clasificación por tipo de parámetros.
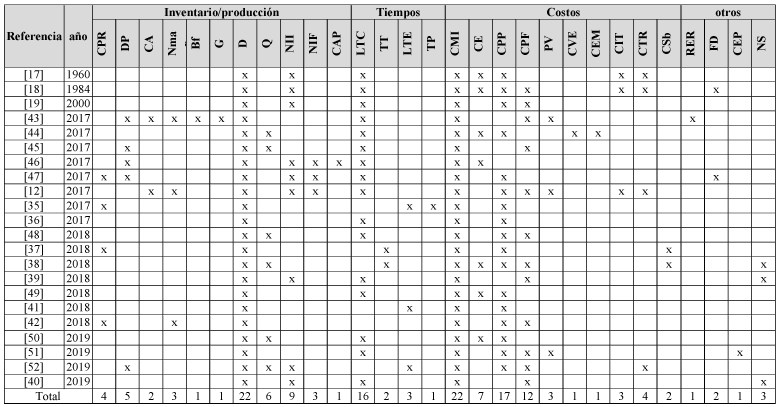
Fuente: Elaboración propia
Parámetros: CPR: Capacidad de procesamiento, DP: Demanda por producto, CA: Capacidad de almacenamiento, Nmax: Número máximo de pedidos, Bf: Porcentaje de defectos, G: Porcentaje desperdicios, D: Demanda, Q: Tamaño de lote, NII: Inventario inicial, NIF: Inventario final, CAP: Capacidad de camiones, LTC: Lead Time constante o cero, TT: Tiempo de transporte, LTE: Lead Time estocástico, TP: Tiempo de producción, CMI: Costo mantenimiento de inventario, CE: Costo de envió, CPP: Costo de pedido pendiente, CPF: Costo de pedir o fabricar, PV: Precio de venta, CVE: Costo variable de envió, CEM: Costo de emisiones por unidad enviada, CIT: Costo de inventario en tránsito, CTR: Costo de transportar, CSb: costo de subcontratar, RER: Recursos económicos, FD: factor de descuento, CEP: coeficiente de esfuerzo promocional, NS: nivel de servicio.
b. Localización
El problema de localización de las instalaciones se considera como una generalización del problema de transporte donde se incluyen costos por la apertura de instalaciones [53], al ser un modelo general de gestión de la CS se relaciona con la gestión de almacenes e inventarios, donde cada problema tiene un conjunto de costos que forman parte del costo total del sistema [54]. En problemas de localización se requiere un conjunto potencial de ubicación de instalaciones y su respectivo conjunto de clientes con demanda por satisfacer [55], estos modelos establecen la ubicación de las instalaciones y asignan los clientes a las mismas [56]. En [57] presentan diferentes aplicaciones en la industria y los servicios, con diversas complejidades como en entidades pública (Hospitales, Central de Bomberos, Estación de policía etc.) que logre una buena relación Cobertura/Costo, en la industrial la cobertura busca la disponibilidad al cliente o la cercanía a los diferentes agentes de la CS. El objetivo de transformar un modelo determinista añadiendo parámetros estocásticos radica en la adaptación y representación de una situación de la vida real ya que algunos parámetros determinísticos en realidad son de naturaleza estocástica [1], los autores desarrollan los modelos estocásticos a partir de uno determinístico, se presenta mayor complejidad del problema a mayor nivel estocástico [2]. Se tuvieron en cuenta los modelos de localización más relevantes, estos son de una sola planta y múltiples plantas, p-mediana y p-Hub, teniendo en cuenta la cobertura y la capacidad.
1. Taxonomía de los modelos de localización
Los modelos fueron clasificados en tres categorias: Según el tipo de problema y características del modelo donde se tiene en cuenta el número de instalaciones, la capacidad y cobertura. La función objetivo que contempla minimización de costo, minimización de tiempos, distancias o riesgos. Métodos de solución según las herramientas, si es programación estocástica, lineal, algoritmos metaheurísticas o lagrangianas, etc. Se concluye con la estocasticidad en el problema. En la Tabla 5 se muestran 20 artículos de modelos estocásticos de localización dónde se presenta el tipo de modelo, las características, función objetivo, métodos de solución y variables estocásticas.
Tabla 5: Taxonomía Localización, tipo de problema, características, estocasticidad y solución.
Referencia |
Año |
Tipo De Problema |
Características |
Estocasticidad |
Función Objetivo |
Solución |
||||||||||||||||||||||||
1 P |
PM |
P H |
M P |
M I |
CA |
N CA |
TR |
P D N S |
MAX CB |
T D |
DE |
C/U |
I R PT |
F E N (P H) |
C V |
MIN CS |
MIN T |
MIN D |
RI |
P E 2 N |
P E |
P MAT |
P L |
LG |
M G |
M M |
R S |
TA |
||
[58] |
1971 |
|
x |
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[59] |
1986 |
x |
x |
|
|
|
|
x |
|
|
|
|
x |
x |
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
[5] |
1998 |
|
x |
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[60] |
2007 |
|
x |
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
[61] |
2009 |
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[62] |
2013 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
x |
|
|
|
|
|
|
|
[63] |
2013 |
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[54] |
2013 |
|
|
|
x |
x |
x |
|
|
|
|
|
x |
|
x |
|
x |
x |
|
|
|
|
|
x |
|
|
|
|
|
|
[64] |
2015 |
|
|
x |
|
|
|
|
x |
|
|
|
x |
|
|
x |
|
x |
|
|
x |
x |
|
|
|
|
|
|
|
|
[65] |
2016 |
|
|
|
|
|
x |
|
|
|
|
|
x |
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
[66] |
2015 |
|
|
x |
|
|
|
x |
x |
|
|
|
x |
x |
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
[56] |
2015 |
|
|
|
|
|
x |
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
[67] |
2015 |
|
|
|
|
|
x |
x |
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
[68] |
2017 |
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
[2] |
2017 |
|
|
|
|
|
|
|
|
|
x |
|
x |
x |
x |
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
x |
[69] |
2017 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
x |
|
x |
|
|
|
|
|
|
x |
x |
x |
|
[70] |
2018 |
|
|
|
|
x |
|
|
|
|
|
|
x |
x |
x |
|
|
x |
x |
|
|
|
|
x |
|
|
x |
|
|
|
[71] |
2018 |
|
|
x |
x |
|
|
|
|
x |
x |
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
[72] |
2018 |
|
|
|
|
|
|
|
|
|
x |
|
x |
|
x |
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
TOTAL |
2 |
4 |
4 |
7 |
2 |
6 |
3 |
2 |
1 |
4 |
2 |
13 |
6 |
6 |
1 |
2 |
6 |
4 |
2 |
1 |
3 |
6 |
3 |
2 |
1 |
2 |
1 |
2 |
1 |
|
Fuente: Elaboración propia.
Notación: 1 P: Una sola planta; PM: P – mediana; PH: P-HUB; M P: Múltiples periodos; M I: Múltiples instalaciones; CA: Capacitado; N CA: No capacitado; TR: Trasbordo; PDNS: Penalización demanda no satisfecha; MAX CB; Máxima cobertura; TD: Tercerización de la demanda; DE: Demanda; C/U: Costo/utilidad; IRPT: Instalaciones requeridas en un periodo t; FEN(PH): Flujo entre nodos (P-HUB); CV: Cobertura variable. MIN CS: Minimización de costo; MIN T: Minimizar tiempo; MIN D: Minimizar distancia; RI: Riesgo; PE2N: Programación estocástica de dos niveles; PE: Programación estocástica; PMAT: Programación matemática; PL: Programación lineal; LG: Lagrange; MG: met. Genético; MM: Memético; RS: Recocido simulado; TA: Tabú.
2. Tipos de modelo
Se clasifican en una planta, p-mediana y P-hubs.
2.1. Ubicación de una sola planta
Los primeros modelos de localización fueron para una planta al establecer el mejor lugar con el fin de satisfacer la demanda, En [59] publicó varios artículos de localización estocástica considerados seminales, estudio el fenómeno de la estocasticidad en los parámetros de demanda y costos de distribución en éste modelo para una planta, implicó no satisfacer completamente la demanda del centro de distribución debido a que no se puede calcular con certeza la demanda. Para dar solución a éste problema Lovelaux calculó el valor esperado de los parámetros estocásticos, determina la localización con su respectivo tamaño y luego asigna las demandas, con programación matemática estocástica de dos niveles [59].
2.2. P-mediana
En éste tipo de problema se requiere ubicar un número P de instalaciones que minimicen el costo de satisfacer demandas específicas. En [59] argumenta que los modelos p-mediana son similares a los modelos de una sola planta, pero se añaden restricciones tales cómo el costo de transporte a un cliente (i) de una instalación (j) de tal manera que se logre la asignación de los clientes a las instalaciones de menor costo. En [59] y [60] trabajan el componente estocástico agregando aleatoriedad en los costos de transporte y las demandas, además plantean escenarios donde la demanda no siempre puede ser satisfecha del todo y agregan costos de penalización.
2.3. P-Hub
Los modelos de localización P-Hub tienen por estructura la unión de las ubicaciones cómo nodos conectados por arcos, a diferencia de modelos de una planta y p-mediana, este modelo genera mayor complejidad al sistema ya que se convierte en un grafo de transferencias entre los diferentes nodos. Se plantean dos tipos de nodos, denominados Hub y No-Hub, los nodos Hub son receptores y transmisores en la CS, es decir, puntos intermedios en la CS y los nodos No-Hub actúan como puntos de origen o destino final de la CS [64]. En [66], plantean un modelo P-Hub donde se añaden múltiples asignaciones a los nodos P-Hub, la aleatoriedad en la demanda y en los costos de transporte, desarrollan un modelo estocástico de dos niveles, tiene como restricción que la aleatoriedad debe ser homogénea para los nodos No-Hub (orígenes y destinos). Los tipos de modelos de localización se observan en la figura 5, algunos trabajos han utilizado más de un tipo de modelo en su investigación, cada circulo compone un tipo de modelo de localización y las intersecciones de los mismos se da por la combinación de los mismos.
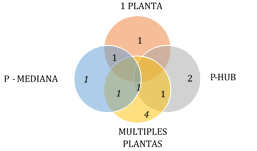
Figura 5: Frecuencia de uso de tipo de modelo de localización.
Fuente: Elaboración propia.
La mayoría de los modelos desarrollados se centran en el tipo de modelo con múltiples plantas (58,3%), seguido de P-HUB y P-mediana (33,3%), por otra parte autores cómo [5], [60] y [71] utilizaron dos o más tipos de modelo en sus trabajos.
2.4. Capacidad
Según su capacidad se encuentran dos tipos: con un número limitado de existencias (capacitados), por ende, la demanda no puede ser cubierta totalmente por la instalación, por otro lado, están los modelos en que las instalaciones no tienen un límite de demanda. Por su parte [56], considera las instalaciones con capacidad finita en un modelo de p-mediana con demanda estocástica, donde las instalaciones solo serán abiertas si pueden abastecer una demanda determinada, minimiza el costo de aperturas de nuevas plantas, se presentan casos en los que la demanda no puede ser satisfecha y entra al problema un parámetro de penalización que equilibran las ecuaciones del modelo. En [65], plantean un modelo P-hub para localización y asignación, contempla el flujo de recursos entre las diferentes instalaciones. En [70] desarrollan un modelo similar con demanda aleatoria y costos de escasez en los nodos, tiene dos funciones objetivos, la primera es balancear el sistema y la segunda minimiza los costos de gestión y de demanda insatisfecha.
2.5. Cobertura
Los problemas de ubicación de instalaciones con cobertura tienen como objetivo ubicar las localizaciones con el fin de suplir las demandas que representadas Las instalaciones tienen la propiedad de cobertura de demandas donde los modelos buscan maximizar la capacidad de cobertura requiriendo el mínimo número de instalaciones y reduciendo los costos, [2] aplican este modelo a los problemas de localización en lugares donde se presentan emergencias, logística humanitaria, la función objetivo es la minimización del riesgo. En [69], minimizan el tiempo de respuesta, las distancias, y los costes de transporte en otro problema de instalaciones en logística humanitaria. [2] y [69] añaden el fenómeno de estocasticidad estableciendo escenarios de emergencia que cuentan con una probabilidad de ocurrencia, donde el número de instalaciones requeridas y la capacidad de cobertura varían en función del tiempo. Autores como [5], [54] y [65] trabajan los problemas de cobertura en sistemas de producción y distribución con demandas estocásticas y los puntos de cobertura varían con funciones de probabilidad; por su parte [72] establecen un modelo de localización de cobertura estocástica combinando el problema de asignación en múltiples periodos.
3. Características
Comprende los múltiples periodos, capacidad y cobertura.
3.1. Múltiples Periodos
Se pueden considerar modelos dinámicos, cuando las demandas varian en función del tiempo, se desarrollan modelos que consideran la apertura o cierre de las instalaciones en un momento determinado en el horizonte de planeación, o que abren y cierran según las condiciones de estacionalidad y fluctuación de la demanda y la no satisfecha es penalizada con un costo de déficit. La localización en múltiples periodos aparece cuando existen parámetros inciertos al inicio del horizonte de planeación y que se pueden ir descubriendo a lo largo del tiempo. Se pueden representar en árboles, cada escenario con una probabilidad asociada [63] y [71].
La figura 6 muestra la frecuencia de uso de las características de los modelos de localización, el 46,1% de los modelos son capacitados, el 30,7% se enfocan en la cobertura y el 15,3% permiten tercerizar la demanda y cuenta con canales de trasbordo.

Figura 6: Frecuencia de uso de características localización
Fuente: Elaboración propia.
c) VRP ( Vehicle Routing Problem)
El problema de enrutamiento de vehículos (VRP, por sus siglas en inglés) es uno de los campos de investigación en logística más estudiado en la literatura. En el VRP se diseña un conjunto de rutas de costo mínimo de una flota de vehículos con capacidad fija para la entrega y recogida, de manera que cada demanda sea atendida por exactamente un vehículo. La demanda total en cada ruta es menor o igual a la capacidad del vehículo asignado y la ruta comienza y termina en el depósito central [73]. Los costos operativos de los vehículos serán altos cuando se utilicen muchos vehículos en muchas rutas pequeñas, la distancia total para el sistema de rutas generalmente aumenta con el número de rutas [7], [8], [74] y [75]. El VRP estocástico (SVRP, por sus siglas en inglés) aparece cuando uno o varios parámetros son inciertos [7], [74] y [76].
1. Taxonomía VRP
La tabla 6 muestra 22 artículos dedicados al estudio de modelos estocásticos de ruteo dónde se presenta la taxonomía mediante el tipo de modelo, las características, función objetivo, métodos de solución y variables estocásticas.
1.1. Tipos de modelo
En concordancia con [7] y [8], para el SVRP se distinguen cuatro tipos de modelos: el VRPSD (VRP Stochastic Demand) es un VRP con demanda estocástica, m de vehículos cuya capacidad limitada atienden clientes con demanda desconocida que puede ser mayor a la capacidad del vehículo. Pueden presentarse dos escenarios: se incurre en costos por déficit al incumplir al cliente o, el vehículo debe retornar al punto de distribución para reaprovisionar la demanda restante [77], [78]. En el VRPSTT (VRP Stochastic Travel Time) cada cliente tiene que ser atendido en una ventana de tiempo [79], el modelo fue introducido por [80] y contempla ventanas de tiempo aleatorias para las rutas, planifica un conjunto de rutas antes de que se conozca el tiempo requerido para atender a cada cliente, de modo que se cumplan con estas restricciones [81]. El VRPSC (VRP stochastic Customer) fue desarrollado por primera vez por [82], es un TSP en donde se conoce la ubicación precisa de los nodos, la probabilidad de que el cliente realice o no un pedido al CD, se representa por p si esta presente o (1-p) ausente. El VRPSDC (VRP Stochastic demand and Customers) es la combinación del VRPSD y el VRPSC, tiene por objetivo la búsqueda de la ruta óptima para un vehículo capacitado que entrega la mercancía a un conjunto de clientes, donde cada cliente tiene una probabilidad fija de ser visitado y una demanda estocástica [83]. Autores cómo Balaprakash et al. [83] desarrollan modelos cuya demanda y clientes son estocásticos.
En la figura 7 se evidencia la frecuencia de uso de los modelos de Ruteo según la taxonomia. La mayoría de autores trabajan sobre modelos cuya demanda es estocástica (52,4%), seguido de modelos con ventanas de tiempo estocásticas (33,3%), el (19%) trabaja con clientes estocásticos.
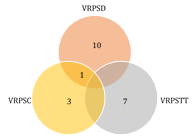
Figura 7: Frecuencia de uso de tipo de modelo en ruteo.
Fuente: Elaboración propia.
Tabla 6: Taxonomía Ruteo, tipo de modelo, características y estocasticidad.
Referencia |
Año |
Tipo De Modelo |
Caracteristicas (Restricciones) |
Estocasticidad |
|||||||||||||||
VRPSD |
VRPSC |
VRPSDC |
VRPSTT |
DIN |
CA |
NO CA |
1V |
MVHO |
MVHET |
RyE |
EP |
DE |
V E |
CS |
ASIM |
CL |
V T |
||
[75] |
1983 |
X |
|
|
|
|
X |
|
X |
X |
|
|
|
X |
|
|
|
|
|
[84] |
1988 |
|
X |
|
|
|
|
X |
X |
|
|
|
|
|
|
|
|
X |
|
[83] |
2015 |
|
|
X |
|
|
X |
|
X |
|
|
|
X |
X |
|
|
|
X |
|
[85] |
2016 |
X |
|
|
|
|
X |
|
|
X |
|
|
|
X |
|
|
|
|
|
[76] |
2016 |
X |
|
|
|
|
|
X |
X |
|
|
|
|
X |
|
|
|
|
|
[86] |
2018 |
X |
|
|
|
|
X |
|
|
X |
|
|
|
X |
X |
|
|
|
|
[77] |
2018 |
X |
|
|
|
X |
X |
|
|
|
|
|
X |
X |
|
|
|
|
|
[87] |
2019 |
|
X |
|
|
X |
|
X |
X |
|
|
|
|
|
X |
|
X |
X |
|
[88] |
2018 |
|
|
|
X |
|
X |
|
|
X |
|
|
|
|
|
|
|
|
X |
[89] |
2018 |
X |
|
|
|
|
X |
|
X |
|
|
|
|
X |
|
|
|
|
|
[90] |
2018 |
X |
|
|
|
|
X |
|
|
X |
|
|
|
X |
X |
|
|
|
|
[91] |
2018 |
|
|
|
X |
|
X |
|
|
X |
|
|
|
|
X |
|
|
|
X |
[78] |
2018 |
X |
|
|
|
|
X |
|
|
X |
|
|
|
X |
|
|
|
|
|
[81] |
2018 |
|
|
|
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
X |
[92] |
2019 |
X |
|
|
|
X |
|
|
X |
|
|
|
|
X |
|
|
|
|
|
[93] |
2018 |
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
X |
X |
[94] |
2018 |
|
|
|
X |
|
X |
|
|
X |
|
X |
|
|
|
|
|
|
X |
[95] |
2018 |
X |
|
|
|
|
X |
|
|
X |
|
|
|
|
|
|
|
|
|
[79] |
2019 |
|
|
|
X |
|
|
X |
X |
|
|
|
|
|
X |
|
X |
|
X |
[96] |
2019 |
|
X |
|
|
X |
X |
|
|
X |
|
|
|
|
X |
|
|
X |
|
[97] |
2019 |
X |
|
|
|
|
X |
|
|
X |
|
|
|
X |
X |
|
|
|
|
[98] |
2019 |
|
|
|
X |
|
X |
|
|
|
X |
|
|
|
X |
X |
|
|
X |
TOTAL |
11 |
3 |
1 |
7 |
5 |
15 |
4 |
8 |
11 |
1 |
1 |
2 |
11 |
8 |
1 |
2 |
5 |
7 |
|
Fuente: Elaboración propia.
Notación: VRPSD: Demanda estocástica, VRPSC, Clientes estocásticos, VRPSDC: Demandas y Clientes estocásticos, VRPSTT, Ventanas de tiempo estocásticas, DIN: Dinámico, CA: Capacitado NO CA: No Capacitado, 1v: 1 Vehículo MVHO: múltiples vehículos Flota homogénea MVHet: múltiples vehículos Flota heterogénea, RyE: Recogida y Entrega, EP: Entregas Parciales, DE: Demanda, V E: Validación Escenarios, CS: Costo, ASIM: Asimétrico, CL: Clientes, VT: Ventanas de Tiempo.
En los últimos años ha tomado relevancia los modelos dinámicos (on-line, off-line). El desarrollo tecnológico ha facilitado la gestión de la flota en tiempo real. Decisiones tomadas antes de la ejecución considerando posibles eventos dinámicos (Off-line) o decisiones que se producen durante un evento dinámico (On-line). El VRPSTT On-line es una estrategia que acepta tardanza en caso de pequeñas desviaciones en los tiempos de viaje, pero reaccionar a eventos de gran magnitud, al considerar la estocasticidad mejora el nivel de servicio sin un impacto negativo en los costos de operación [76].
Los autores en [96] considera un VRPSC con flota homogénea y política de entrega el mismo día (SDD), contempla la forma dinámica de aparición de clientes y da la posibilidad de aceptar o no nuevas solicitudes, se soluciona con dos algoritmos basados en Branch and Price. A la luz de esta revisión de la literatura, se ha evidenciado que las investigaciones respecto a la toma de decisiones en tiempo real para los SVRP son escasas y con el rápido desarrollo tecnológico, se hace indispensable profundizar en esta línea de investigación.
1.2. Capacidad en los vehículos.
En la literatura se hace una distinción entre los problemas de ruteo capacitados (VRP) y no capacitados (TSP) siendo VRP una extensión de TSP [7]. En [79] proponen un SVRP no capacitado con tiempos de viaje inciertos a lo largo de los arcos para determinar la ruta en ventanas de tiempo estipuladas, para lo cual incluyen un nuevo criterio de decisión que penaliza el nivel de servicio. Por su parte [87], consideran un problema SDD de una red de distribución local con un solo vehículo, existe incertidumbre en la ubicación de los clientes, ya que estos van apareciendo mientras el vehículo cubre otra ruta, por esto se hace necesario que el vehículo vuelva al depósito para aprovisionarse antes de servir a los nuevos clientes, además considera los costos asimétricos y su objetivo es minimizar el tiempo e impacto ambiental.
El estudio presentado por [91] consideran un VRPSTT con restricciones de carga, la demanda de los clientes está en items no apilables, ejemplo muebles o maquinaria, se limita la capacidad del vehículo por peso, forma o fragilidad de la mercancía. Desarrollan una metodología capaz de generar mejores soluciones para escenario en condiciones de incertidumbre, con el objetivo de minimizar los costos y el tiempo de recorrido. En [86] modelan un VRPSD con restricción de capacidad y encuentran el número de vehículos necesarios a asignar a un conjunto de clientes. Lo solucionan mediante 5 métodos exactos diferentes donde asumen la demanda estocástica y correlacionada.
1.3. Sobre la flota.
La flota tiene en cuenta la cantidad de vehículos y si son homogéneos o heterogéneos. En los modelos de un sólo vehículo se busca dirigir dinámicamente un vehículo para servir a todas las solicitudes realizadas la comienzo del día de trabajo y la mayor cantidad de solicitudes que llegan durante la jornada de trabajo como sea posible [92], algunos autores contemplan la necesidad del vehículo de volver al deposito para reaprovisionar [85].
Los modelos en donde el número de vehículos es mayor a 1 se consideran decisiones de asignación y cantidad de rutas a un grupo de vehículos o de manera individual. En [75], la función objetivo incluye la decisión de asignar rutas largas para un conjunto de vehículos o diseñar rutas más cortas para cada vehículo, los cuales cuentan con diferentes capacidades. Por su parte [88], plantean un modelo para vehículos homogéneos, mientras [98] presentan un modelo VRPSTT con flota heterogénea respecto a su capacidad, consideran los costos y tiempos de viaje aleatorios para una distribuidora de chocolates y confitería. El objetivo es minimizar costos y maximizar el nivel de servicio a los clientes, en una metaheurística de colonia de abejas artificial (ABC).
1.4. Políticas de ruteo.
Existen dos tipos de modelos VRP con demanda estocástica, aquellos que se resuelven asegurando una probabilidad de falla en la ruta por debajo de cierto nivel y los modelos que consideran políticas de recursos, las cuales describen las acciones a tomar con el fin de reparar la solución después de un fracaso en la ruta [99]. En [90] consideran un VRPSD con un solo depósito y flota homogénea, modela una política de recurso clásica que consiste en volver al depósito cuando falle la ruta, de forma que vuelve al nodo y reanuda la ruta. Proponen un algoritmo hibrido de dos metaheurísticas que logran resolver problemas muy grandes en tiempos pequeños.
Los autores en [97] asumen que la demanda del cliente solo se conoce a la llegada del vehículo (VRPSD) y plantean una política de acción de recurso proactiva, si el residual de la capacidad del vehículo está por debajo de cierto nivel entonces el camión debe volver al depósito para aprovisionarse y luego continuar con la ruta. En comparación con la política de recurso clásica reactiva, demuestra que una política con reglas definidas, disminuyen el número de fallas en la ruta.
1.5. Ruteo con entrega y recogida
Las comparaciones entre las soluciones obtenidas por el modelo estocástico y determinista han validado las ventajas y robustez de considerar los tiempos de viaje y de servicios estocásticos [77]. En ese sentido,[94] presentan un caso de estudio para una empresa de cuidados de la salud, modelan con programación estocástica un problema de VRPSTT con entrega de medicamentos e instrumentos y recogida de desecho y pruebas de laboratorio.
La figura 8 muestra la distribución de los artículos según la frecuencia, se tiene en cuenta las características en los respectivos modelos.

Figura 8: Frecuencia de uso de características de los modelos de ruteo.
Fuente: Elaboración propia.
En términos de capacidad el 78,9% de los autores incluidos en la presente revisión, se basan en modelos capacitados, el 60,0% trabaja con una flota múltiple de vehículos y el 8,3% de aquellos cuenta con vehículos heterogéneos. En la tabla 7 se presenta la clasificación de los modelos de ruteo según función objetivo y métodos de solución.
Tabla 7: Taxonomía ruteo, función objetivo y solución.

Fuente: Elaboración propia.
Notación: MIN CS: Minimización de costo; MIN T: Minimización de tiempos; MIN D: Minimización de distancia, N Ser: Nivel de Servicio, AMB: Nivel Ambiental, P E2 N: Programación estocástica de dos niveles; P E: Programación estocástica; P MAT: Programación matemática; P L: Programación lineal, OP ROB: Optimización Robusta, OPET: Optimización Enteros Mixtos, A2E: Algoritmo 2 etapas, HEU: Alg basados en heurísticas, ME Métodos exactos, M Ben: desc benders, MMEM Metaheurística Memética, R S: Recosido Simulado, TAB: Búsqueda Tabú, P DIN: Programación dinámica, M BU: Metaheurística búsqueda local iterativa, MCH: Metaheurística Colonia de Hormigas, OMH: Otras metaheurística, SIM: Simulación.
En este aparte se presentan las funciones objetivo de los modelos. La figura 9 muestra la frecuencia de uso de funciones objetivo, incluyen costo, tiempo, distancia y otros, el subconjunto otros, está conformado por variables de decisión cómo riesgo, nivel de servicio y nivel de inventario.
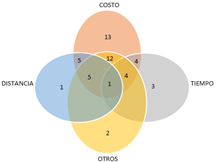
Figura 9: Frecuencia de uso de función objetivo del total de artículos.
Fuente: Elaboración propia.
Al momento de definir la función objetivo en los modelos logísticos, el costo es la medida de desempeño más tenida en cuenta en el 84% de los problemas citados. El tiempo y la distancia son considerados en el 25% de los casos, la suma de los criterios que conforman el subconjunto Otros son tenidos en cuenta en el 45% de los modelos, el cual está compuesto en 29% en nivel de inventario, 12% maximizar el nivel de servicio, 2% Minimizar el impacto ambiental y el 2% restante en la minimización del riesgo.
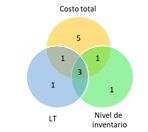
Figura 10: Función objetivo – Frecuencia en modelos de inventarios.
Fuente: Elaboración propia.
La figura 10, 11 y 12 muestran la clasificación por objetivos para cada modelo, en inventario se tiene en cuenta el costo, tiempo y nivel de inventario, para localización, costo, riesgo tiempo y distancia, y para ruteo se tiene en cuenta costo, distancia, tiempo, nivel de servicio y factor ambiental.
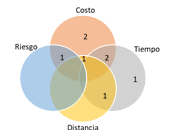
Figura 11: Función objetivo – Frecuencia modelos de localizacion.
Fuente: Elaboración propia.
En los artículos de inventarios el nivel de existencias es calculado como objetivo en el 68,2%, la distancia también es representativo en los modelos de localización (25%) y ruteo (52,4%).
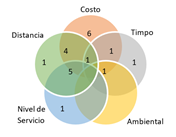
Figura 12. Función objetivo – Frecuencia modelos de ruteo.
Fuente: Elaboración propia.
La investigación en el campo de los modelos logísticos con componentes estocásticos es relevante en el mundo académico; una razón es la complejidad en la búsqueda de los métodos de solución, este tipo de problemas difícilmente son optimizables, se buscan soluciones factibles y aproximadas a un valor optimo [8]. En la figura 13 se aprecian los métodos de solución utilizados, siendo los métodos exactos (44%) la más utilizada, le siguen las metaheurísticas (25%), heurísticas (24%) y la simulación (7%). Los métodos de optimización exacta son utilizados como base para validar el modelo en instancias pequeñas y comparar el desempeño y calidad de solución de los algoritmos empleados por los autores.
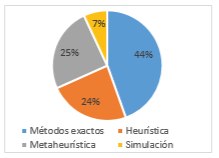
Figura 13: Porcentaje de uso métodos de solución – Los tres modelos.
Fuente: Elaboración propia.
Algunos autores emplean más de un método de solución, los porcentajes presentados se obtuvieron con base en la cantidad de veces que se empleó un método de solución para encontrar un resultado al problema. Existen diferentes metodologías para establecer los valores de entrada a los algoritmos, se evidencia el uso frecuente del método Taguchi para la determinación de los parámetros iniciales de las metaheurísticas empleadas y el uso de diferentes métricas para comparar la efectividad de los métodos de solución [100].
En la figura 14, 15 y 16 se presenta el porcentaje en el uso de métodos de solución para cada modelo de toma de decisiones logísticas. En localización el método de solución más utilizado es la optimización con 67%, de los cuales la programación estocástica se usa en el (43%), la programación estocástica de dos niveles en (21%) y programación matemática en (21%). Por su parte las metaheurísticas son usadas el (28%), en las que los más usados son los AG que representan el (33%) y el Recocido Simulado (33%). A la luz de esta revisión, no se evidencio el uso de la simulación como método de solución para los problemas de localización, lo que puede sugerir un enfoque interesante para trabajos futuros, figura 14.

Figura 14: Porcentaje de uso de los métodos de solución – Localizacion.
Fuente: Elaboración propia.
En los modelos de inventario multieslabón las heurísticas de dos fases (43%) y las basadas en descomposición (35%) son las más utilizadas. Le siguen los métodos exactos (15%), la simulación (11%) y las metaheurísticas (7%), siendo el AG y el AAB las metaheurísticas utilizadas, figura 15.
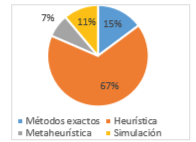
Figura 15: Porcentaje de uso de los métodos de solución – Inventario.
Fuente: Elaboración propia.
El estudio presentado por [48] proponen un método heurístico de solución mediante un algoritmo de procedimiento iterativo para definir lo inventarios en CS cerradas. Mientras [49] aplican el algoritmo WWK, un algoritmo para calcular el nivel optimo de inventario a un solo cliente servido por un proveedor que loa abastece con una probailidad a, para un eslabón y comprobar su desempeño, demuestran que tiene un despliegue efectivo y encuentra una solución óptima para dos eslabones con costos y demanda con incertidumbre.
En el nivel operativo VRP, se usan métodos de solución exactos con más frecuencia (51%), en instancias pequeñas para validar la solución propuesta. Las instancias medias o grandes generalmente se resuelven mediante metaheurísticas o algoritmos híbridos (32%), combinando metaheurísticas [90], o mezclando una metaheurística y una heurística [91]. Las metaheurísticas más utilizadas son Algoritmos meméticos (35%) y Búsqueda Tabu (18%). Si bien los tres modelos pertenecen a la clase NP-Hard, el campo de investigación en VRP presenta una complejidad superior a los modelos de inventario y localización que despierta interés por desarrollar más y mejores métodos de solución, figura 16.
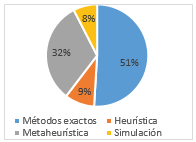
Figura 16: Porcentaje de uso de los métodos de solución – VRP.
Fuente: Elaboración propia.
Los modelos logísticos estocásticos acercan la planificación empresarial a la realidad. El artículo muestra la integración de los parámetros de aleatoriedad en los modelos de localización, inventario y enrutamiento. Se presentan nuevos modelos individuales logísticos estocásticos que permiten tomar mejores decisiones a corto, mediano y largo plazo.
Varios autores destacan la necesidad de desarrollar nuevos algoritmos y métodos de solución más eficientes para modelos complejos, grandes instancias en las que hay muchos actores en cada eslabón, instancias en las que actualmente no es posible tomar decisiones debido a un gran tiempo de cálculo y costo computacional.
Trabajos futuros prometedores en estos tres campos de investigacion pueden incluir el desarrollo de modelos multiobjetivo considerando, además de lo económico, factores ambientales, sociales, humanitarios y de riesgo. Implementación de técnicas de la ciencia de la computación como la inteligencia artificial en los métodos de solución podrian ser interesantes.
En la tabla 8 se presenta los trabajos futuros identificados en la revisión de la literatura, se enuncian según los tres modelos presentados.
Tabla 8: Trabajos Futuros.
MODELOS |
TRABAJOS FUTUROS |
Inventario |
Se ha identifica la necesidad de estudiar el LT incierto en modelos multieslabón, más aún el problema de cruce de ordenes multieslabón [25] [26] [27]. Sistemas de producción/inventario con varios centros de distribución [35] y procesos de remanufacturación con consideraciones ambientales [42]. |
Localización |
Existe la necesidad investigar problemas en situaciones específicas de localización, con atención especial a los casos de logística humanitaria en la que se deben tomar decisiones de ubicación de centros de abastecimiento y atención en situaciones de desastres naturales y emergencias humanitarias [2] [69] |
Ruteo |
Respecto al modelado de los problemas VRP se plantea definir nuevas políticas de recursos [86] [95] con importancia en los aspectos ambientales [83]. Con el incremento en la complejidad de los modelos estocásticos, los autores apuntan su interés a métodos de solución metaheurísticos mejorando el tiempo de cálculo [91] [94]. Se plantean la necesidad de algoritmos híbridos entre metaheurísticas y técnicas de simulación [86] |
Fuente: Elaboración propia.
[1] A. Devin, S. Fayyaz, and R. Sadeghi, “Stochastic facilities location model by using Stochastic programming,” Shiraz J. Syst. Manag., vol. 1, pp. 59–71, 2013.
[2] C. Boonmee, M. Arimura, and T. Asada, “Facility location optimization model for emergency humanitarian logistics,” Int. J. Disaster Risk Reduct., vol. 24, pp. 485–498, 2017. https://doi.org/10.1016/j.ijdrr.2017.01.017.
[3] A. T. Gumus and A. F. Guneri, “Multi-echelon inventory management in supply chains with uncertain demand and lead times : literature review from an operational research perspective,” J. Eng. Manuf., vol. 221, pp. 1553–1570, 2007. https://doi.org/10.1243/09544054JEM889.
[4] D. Simchi-levi and Y. Zhao, “Performance Evaluation of Stochastic Multi-Echelon Inventory Systems : A Survey,” Adv. Oper. Res., vol. 2012, pp. 1–33, 2012. https://doi.org/10.1155/2012/126254.
[5] S. H. Owen and M. S. Daskin, “Strategic facility location: A review,” Eur. J. Oper. Res., vol. 111, no. 3, pp. 423–447, 1998. https://doi.org/10.1016/S0377-2217(98)00186-6.
[6] M. T. Melo, S. Nickel, and F. Saldanha-da-Gama, “Facility location and supply chain management - A review,” Eur. J. Oper. Res., vol. 196, no. 2, pp. 401–412, 2009. https://doi.org/10.1016/j.ejor.2008.05.007.
[7] L. B. Rocha Medina, E. C. González La Rota, and J. A. Orjuela Castro, “Una revisión al estado del arte del problema de ruteo de vehículos : Evolución histórica y métodos de solución,” Ingeniería, vol. 16, no. 2, pp. 35–55, 2011.
[8] E. C. Gonzalez la Rotta, O. Gonzalez, and M. Becerra, “ESTADO DEL ARTE DEL PROBLEMA DE RUTEO DE VEHÍCULOS CON COMPONENTES ESTOCÁSTICOS THE,” Inventum, vol. 13, pp. 2–13, 2018. https://doi.org/10.26620/uniminuto.inven.
[9] D. L. Rincón, J. E. Fonseca Ramirez, and J. A. Orjuela Castro, “Towards a common reference framework for traceability in the food supply chain,” Ingenieria, vol. 22, no. Xx, pp. 1–25, 2017. http://dx.doi.org/10.14483/udistrital.jour.reving.2017.2.a01.
[10] M. E. Palmer Gato, M. Cardos, E. Babiloni, and E. Guijarro, “Revisión de modelos de gestión de inventarios para repuestos reparables,” in 4th International Conference on Industrial Engineering and Industrial Management XIV Congreso de Ingeniería de Organización, 2010, pp. 1329–1335.
[11] J. A. Orjuela-Castro, M. A. Cardona-Rojas, and L. V. Castañeda-López, “Agricultural Supply Chain Mango Inventory Model,” Rev. Ingeneria Ind., vol. 16, no. 2, pp. 141–150, 2017. https://doi.org/10.22320/s07179103/2017.09.
[12] A. Keshari, N. Mishra, N. Shukla, S. Mcguire, and S. Khorana, “Multiple order-up-to policy for mitigating bullwhip effect in supply chain network,” Ann. Oper. Res., vol. 269, no. 1, pp. 361–386, 2018. https://doi.org/10.1007/s10479-017-2527-y.
[13] J. P. Escorcia, R. Amaya Mier, and M. Soto Ferrari, “Métricas desagregadas para la medición del impacto de una política de administración de inventario multi-eslabón,” in Eleventh LACCEI Latin American and Caribbean Conference for Engineering and Technology (LACCEI’2013), 2013, pp. 1–10.
[14] S. M. Disney, A. Maltz, X. Wang, and R. D. H. Warburton, “Inventory Management for Stochastic Lead Times with Order Crossovers,” Eur. J. Oper. Res., vol. 248, pp. 473–486, 2016. https://doi.org/10.1016/j.ejor.2015.07.047.
[15] X. Wang and S. M. Disney, “The bullwhip effect : Progress , trends and directions,” Eur. J. Oper. Res., vol. 250, pp. 691–701, 2016. https://doi.org/10.1016/j.ejor.2015.07.022.
[16] N. Rodríguez Cifuentes, J. Soriano, and J. Orjuela, “Consecuencias del Efecto Bullwhip al implementar la estrutura Vendor Managed Inventory,” in Tenth LACCEI Latin American and Caribbean Conference (LACCEI’2012), Megaprojects: Building Infrastructure by fostering engineering collaboration, efficient and effective integration and innovative planning, 2012, pp. 1–10.
[17] A. J. Clark and H. Scarf, “Optimal Policies for a Multi-Echelon Inventory Problem,” Manage. Sci., vol. 6, no. 4, pp. 475–490, 1960. https://doi.org/10.1287/mnsc.6.4.475.
[18] A. W. I. Federgruen and P. Zipkin, “Computational Issues in an Infinite-Horizon, Multiechelon Inventory Model,” Oper. Res., vol. 32, no. 4, pp. 818–836, 1984.
[19] F. Chen, “OPTIMAL POLICIES FOR MULTI-ECHELON INVENTORY PROBLEMS WITH BATCH ORDERING,” Oper. Res., vol. 48, no. 3, pp. 376–389, 2000.
[20] A. S. Eruguz, E. Sahin, Z. Jemai, and Y. Dallery, “A Comprehensive Survey of Guaranteed-Service Models for Multi- Echelon Inventory Optimization,” Intern. J. Prod. Econ., vol. 117, pp. 110–125, 2016. https://doi.org/10.1016/j.ijpe.2015.11.017.
[21] T. De Kok et al., “A typology and literature review on stochastic multi-echelon inventory models,” Eur. J. Oper. Res., vol. 269, pp. 955–983, 2018. https://doi.org/10.1016/j.ejor.2018.02.047.
[22] V. Gutierrez and C. J. Vidal, “Modelos de Gestión de Inventarios en Cadenas de Abastecimiento : Revisión de la Literatura Inventory Management Models in Supply Chains : A Literature Review,” Rev. Fac. Ing. Univ. Antioquia, vol. 43, pp. 134–149, 2008.
[23] C. K. Gudum, “A new compound lead time demand distribution approach and comparison study,” Res. Pap. Copenhagen Bus. Sch. Denmark, pp. 1–30, 2003.
[24] J. Riezebos, “Inventory order crossovers,” Int. J. Prod. Econ., vol. 104, pp. 666–675, 2006. https://doi.org/10.1016/j.ijpe.2004.11.011.
[25] A. Srivastav and S. Agrawal, “Multi-objective optimization of mixture inventory system experiencing order crossover,” Ann. Oper. Res., pp. 1–18, 2018. https://doi.org/10.1007/s10479-017-2744-4.
[26] Ç. Metin and S. Luo, “Stochastic inventory system with lead time flexibility : offered by a manufacturer / transporter,” J. Oper. Res. Soc., vol. 68, no. 12, pp. 1533–1552, 2017. https://doi.org/10.1057/s41274-016-0172-5.
[27] A. Thorsen and T. Yao, “Robust inventory control under demand and lead time uncertainty,” Ann. Oper. Res., vol. 257, no. 1, pp. 207–236, 2017. https://doi.org/10.1007/s10479-015-2084-1.
[28] R. F. Roldán, R. Basagoiti, and L. C. Coelho, “A survey on the inventory-routing problem with stochastic lead times and demands,” J. Appl. Log., vol. 24, pp. 15–24, 2017. 10.1016/j.jal.2016.11.010.
[29] E. Yadollahi, E. H. Aghezzaf, J. Walraevens, B. Raa, and D. Claeys, “Evaluating approximate solution models for the stochastic periodic inventory routing problem,” J. Manuf. Syst., vol. 50, pp. 25–35, 2019. 10.1016/j.jmsy.2018.11.001.
[30] C. Gonzalez Quitian and J. Nirves Pinzon, “Solucion del problema de optimizacion de inventario de dos escalones con demanda estocastica para una red de distribucion de un solo producto,” 2018.
[31] E. A. Silver, D. F. Pyke, and D. J. Thomas, Inventory and Production Management in Supply Chains. Fourth Edition. | Boca Raton : Taylor & Francis, 2017. | Revised: CRC Press, 2016. 10.1201/9781315374406.
[32] F. Chen, A. Federgruen, and Y.-S. Zheng, “Coordination Mechanisms for a Distribution System with One Supplier and Multiple Retailers,” Manage. Sci., vol. 47, no. 5, pp. 693–708, May 2001. https://doi.org/10.1287/mnsc.47.5.693.10484.
[33] V. Gaur and M. L. Fisher, “A Periodic Inventory Routing Problem at a Supermarket Chain,” Oper. Res., vol. 52, no. 6, pp. 813–822, Dec. 2004. https://doi.org/10.1287/opre.1040.0150.
[34] X. Zheng, M. Yin, and Y. Zhang, “Integrated optimization of location, inventory and routing in supply chain network design,” Transp. Res. Part B Methodol., vol. 121, pp. 1–20, 2019. 10.1016/j.trb.2019.01.003.
[35] A. G. Zare, H. Abouee-mehrizi, and O. Berman, “Exact Analysis of the ( R , Q ) Inventory Policy in a Two-Echelon Production-Inventory System,” Oper. Res. Lett., vol. 45, no. 4, pp. 308–314, 2017. https://doi.org/10.1016/j.orl.2017.04.011.
[36] Y. Rong, Z. Atan, and L. V Snyder, “Heuristics for Base-Stock Levels in Multi-Echelon,” Prod. Oper. Manag., vol. 26, no. 9, pp. 1760–1777, 2017. https://doi.org/10.1111/poms.12717.
[37] T. Aouam and K. Kumar, “On the effect of overtime and subcontracting on supply chain safety stocks,” Omega, vol. 89, pp. 1–20, 2018. https://doi.org/10.1016/j.omega.2018.09.010.
[38] N. De Smet, E. Aghezzaf, and B. Desmet, “Optimising installation ( R , Q ) policies in distribution networks with stochastic lead times : a comparative analysis of guaranteed- and stochastic service models,” Int. J. Prod. Res., pp. 1–18, 2018. https://doi.org/10.1080/00207543.2018.1518606.
[39] N. Sakulsom and W. Tharmmaphornphilas, “Periodic-Review Policy for a 2-Echelon Inventory Problem with Seasonal Demand,” Eng. J., vol. 22, no. 6, pp. 117–134, 2018. https://doi.org/10.4186/ej.2018.22.6.117.
[40] N. Sakulsom and W. Tharmmaphornphilas, “Heuristics for a periodic-review policy in a two-echelon inventory problem with seasonal demand,” Comput. Ind. Eng., vol. 133, pp. 292–302, 2019. https://doi.org/10.1016/j.cie.2019.05.017.
[41] C. Cheng and L. Tang, “Robust policies for a multi-stage production / inventory problem with switching costs and uncertain demand,” Int. J. Prod. Res., vol. 7543, pp. 1–19, 2018. https://doi.org/10.1080/00207543.2017.1413257.
[42] H. Zhu, Y. F. Chen, M. Hu, and Y. Yang, “A Simple Heuristic Policy for Stochastic Distribution Inventory Systems with Fixed Costs,” Rotman Sch. Manag. Work. Pap., no. 2921743, pp. 1–45, 2019.
[43] A. Gharaei, H. S. R. Pasandideh, and S. T. Akhavan, “An optimal integrated lot sizing policy of inventory in a bi-objective multi-level supply chain with stochastic constraints and imperfect products,” J. Ind. Prod. Eng., vol. 35, pp. 6–20, 2017. https://doi.org/10.1080/21681015.2017.1374308.
[44] O. Stenius, J. Marklund, and S. Axs, “Sustainable Multi-echelon Inventory Control with Shipment Consolidation and Volume Dependent Freight Costs,” Eur. J. Oper. Res., vol. 267, pp. 904–916, 2017. https://doi.org/10.1016/j.ejor.2017.12.029.
[45] L. Li, S. Song, C. Wu, and K. You, “Ordering Control in Multi-Stage Multi-Item Supply Chain with Stochastic Demand,” in 13th IEEE International Conference on Control & Automation (ICCA), 2017, pp. 707–712.
[46] Y. Bo, M. Dawande, G. Janakiraman, and S. T. Mccormick, “On Integral Policies in Deterministic and Stochastic Distribution Systems,” Oper. Res., vol. 65, pp. 703–711, 2017.
[47] A. Angelus and W. Zhu, “Looking Upstream : Optimal Policies for a Class of Capacitated Multi-Stage Inventory Systems,” Prod. Oper. Manag., vol. 26, no. 11, pp. 2071-2088., 2017. https://doi.org/10.1111/poms.12742.
[48] B. K. Mawandiya, J. K. Jha, and J. J. Thakkar, “Optimal production ‑ inventory policy for closed ‑ loop supply chain with remanufacturing under random demand and return,” Oper. Res., pp. 1–42, 2018. https://doi.org/10.1007/s12351-018-0398-x.
[49] R. E. King, W. Wangwatcharakul, and D. Warsing Jr., “Computing Base-stock Levels for a Two-Stage Supply Chain with Uncertain Supply,” Omega, vol. 89, pp. 92–109, 2018. https://doi.org/10.1016/j.omega.2018.10.001.
[50] L. Johansson, D. R. Sonntag, J. Marklund, and G. P. Kiesmüller, “Controlling distribution inventory systems with shipment consolidation and compound Poisson demand,” Eur. J. Oper. Res., vol. 280, no. 1, pp. 90–101, 2019. https://doi.org/10.1016/j.ejor.2019.06.045.
[51] S. Ebrahimi, S.-M. Hosseini-Motlagh, and M. Nematollahi, “Proposing a delay in payment contract for coordinating a two-echelon periodic review supply chain with stochastic promotional effort dependent demand,” Int. J. Mach. Learn. Cybern., vol. 10, no. 5, pp. 1037–1050, 2019. https://doi.org/10.1007/s13042-017-0781-6.
[52] D. Das, N. Baran, and V. Jain, “Optimization of stochastic , ( Q , R ) inventory system in multi ‑ product , multi ‑ echelon , distributive supply chain,” J. Revenue Pricing Manag., vol. 18, no. 5, pp. 405–418, 2019. https://doi.org/10.1057/s41272-019-00204-7.
[53] J. A. Orjuela-Castro, L. A. Sanabria-Coronado, and A. M. Peralta-Lozano, “Coupling facility location models in the supply chain of perishable fruits,” Res. Transp. Bus. Manag., vol. 24, no. August, pp. 73–80, 2017. https://doi.org/10.1016/j.rtbm.2017.08.002.
[54] N. Gülpinar, D. Pachamanova, and E. Çanakoglu, “Robust strategies for facility location under uncertainty,” Eur. J. Oper. Res., vol. 225, no. 1, pp. 21–35, 2013. https://doi.org/10.1016/j.ejor.2012.08.004.
[55] L. A. Sanabria Coronado, A. M. Peralta Lozano, and J. A. Orjuela, “Facility Location Models in Perishable Agri-Food Chains: a Review,” Ingeniería, vol. 22, no. 1, p. 65, 2017. https://doi.org/10.14483/udistrital.jour.reving.2017.1.a04.
[56] M. Bieniek, “A note on the facility location problem with stochastic demands,” Omega, vol. 55, pp. 53–60, 2015. https://doi.org/10.1016/j.omega.2015.02.006.
[57] S. Karabay, E. Köse, M. Kabak, and E. Ozceylan, “Mathematical Model and Stochastic Multi-Criteria Acceptability Analysis for Facility Location Problem,” PROMET - Traffic&Transportation, vol. 28, no. 3, pp. 245–256, 2016. https://doi.org/10.7307/ptt.v28i3.1843.
[58] C. Toregas, R. Swain, C. ReVelle, and L. Bergman, “The Location of Emergency Service Facilities,” Oper. Res., vol. 19, no. 6, pp. 1363–1373, Oct. 1971. https://doi.org/10.1287/opre.19.6.1363.
[59] F. Louveaux, “Discrete stochastic location models,” Ann. Oper. Res., vol. 6, pp. 21–34, 1986.
[60] L. V. Snyder, M. S. Daskin, and C. P. Teo, “The stochastic location model with risk pooling,” Eur. J. Oper. Res., vol. 179, no. 3, pp. 1221–1238, 2007. https://doi.org/10.1016/j.ejor.2005.03.076.
[61] C. K. Y. Lin, “Stochastic single-source capacitated facility location model with service level requirements,” Int. J. Prod. Econ., vol. 117, no. 2, pp. 439–451, 2009. https://doi.org/10.1016/j.ijpe.2008.11.009.
[62] N. Ghaffari-Nasab, M. S. Jabalameli, M. B. Aryanezhad, and A. Makui, “Modeling and solving the bi-objective capacitated location-routing problem with probabilistic travel times,” Int. J. Adv. Manuf. Technol., vol. 67, no. 9–12, pp. 2007–2019, 2013. https://doi.org/10.1007/s00170-012-4627-9.
[63] M. Albareda-Sambola, A. Alonso-Ayuso, L. F. Escudero, E. Fernández, and C. Pizarro, “Fix-and-Relax-Coordination for a multi-period location-allocation problem under uncertainty,” Comput. Oper. Res., vol. 40, no. 12, pp. 2878–2892, 2013. https://doi.org/10.1016/j.cor.2013.07.004.
[64] T. Ahmadi, H. Karimi, H. Davoudpour, and S. A. Hosseinijou, “A robust decision-making approach for p-hub median location problems based on two-stage stochastic programming and mean-variance theory: a real case study,” Int. J. Adv. Manuf. Technol., vol. 77, no. 9–12, pp. 1943–1953, 2015. https://doi.org/10.1007/s00170-014-6569-x.
[65] M. Alizadeh, N. Mahdavi-Amiri, and S. Shiripour, “Modeling and solving a capacitated stochastic location-allocation problem using sub-sources,” Soft Comput., vol. 20, no. 6, pp. 2261–2280, 2016. https://doi.org/10.1007/s00500-015-1640-6.
[66] A. Adibi and J. Razmi, “2-Stage stochastic programming approach for hub location problem under uncertainty: A case study of air network of Iran,” J. Air Transp. Manag., vol. 47, pp. 172–178, 2015. https://doi.org/10.1016/j.jairtraman.2015.06.001.
[67] I. Correia and F. Saldanha, “Facility Location Under Uncertainty,” in Location Science, 2015, pp. 177–203. https://doi.org/10.1007/978-3-319-13111-5.
[68] L. P. Melo, F. K. Miyazawa, L. L. C. Pedrosa, and R. C. S. Schouery, “Approximation algorithms for k-level stochastic facility location problems,” J. Comb. Optim., vol. 34, no. 1, pp. 266–278, 2017. https://doi.org/10.1007/s10878-016-0064-2.
[69] M. Golabi, S. M. Shavarani, and G. Izbirak, “An edge-based stochastic facility location problem in UAV-supported humanitarian relief logistics: a case study of Tehran earthquake,” Nat. Hazards, vol. 87, no. 3, pp. 1545–1565, 2017. https://doi.org/10.1007/s11069-017-2832-4.
[70] S. Shiripour and N. Mahdavi-Amiri, “Bi-objective location problem with balanced allocation of customers and Bernoulli demands: two solution approaches,” Soft Comput., pp. 1–20, 2018. https://doi.org/10.1007/s00500-018-3163-4.
[71] L. F. Escudero, M. A. Garín, C. Pizarro, and A. Unzueta, “On efficient matheuristic algorithms for multi-period stochastic facility location-assignment problems,” Comput. Optim. Appl., vol. 70, no. 3, pp. 865–888, 2018. https://doi.org/10.1007/s10589-018-9995-0.
[72] A. Marín, L. I. Martínez-Merino, A. M. Rodríguez-Chía, and F. Saldanha-da-Gama, “Multi-period stochastic covering location problems: Modeling framework and solution approach,” Eur. J. Oper. Res., vol. 268, no. 2, pp. 432–449, 2018. https://doi.org/10.1016/j.ejor.2018.01.040.
[73] J. A. Orjuela-Castro, J. P. Orejuela-Cabrera, and W. Adarme-Jaimes, “Last mile logistics in mega-cities for perishable fruits,” J. Ind. Eng. Manag., vol. 12, no. 2, pp. 318–327, 2019. https://doi.org/10.3926/jiem.2770.
[74] J. Oyola, H. Arntzen, and D. L. Woodruff, “The stochastic vehicle routing problem, a literature review, part I: models,” EURO J. Transp. Logist., vol. 7, no. 3, pp. 193–221, 2018. https://doi.org/10.1007/s13676-016-0100-5.
[75] W. R. Stewart and B. L. Golden, “Stochastic vehicle routing: A comprehensive approach,” Eur. J. Oper. Res., vol. 14, no. 4, pp. 371–385, 1983. https://doi.org/10.1016/0377-2217(83)90237-0.
[76] U. Ritzinger, J. Puchinger, and R. F. Hartl, “A survey on dynamic and stochastic vehicle routing problems,” Int. J. Prod. Res., vol. 54, no. 1, pp. 215–231, 2016. https://doi.org/10.1080/00207543.2015.1043403.
[77] M. Noorizadegan and B. Chen, “Vehicle routing with probabilistic capacity constraints,” Eur. J. Oper. Res., vol. 270, no. 2, pp. 544–555, 2018. https://doi.org/10.1016/j.ejor.2018.04.010.
[78] L. Chen, W. C. Chiang, R. Russell, J. Chen, and D. Sun, “The Probabilistic Vehicle Routing Problem with Service Guarantees,” Transp. Res. Part E Logist. Transp. Rev., vol. 111, no. February, pp. 149–164, 2018. https://doi.org/10.1016/j.tre.2018.01.012.
[79] Y. Zhang, R. Baldacci, M. Sim, and J. Tang, “Routing optimization with time windows under uncertainty,” Math. Program., vol. 175, no. 1–2, pp. 263–305, 2019. https://doi.org/10.1007/s10107-018-1243-y.
[80] G. Laporte, F. Louveaux, and H. Mercure, “The Vehicle Routing Problem with Stochastic Travel Times,” Front. Artif. Intell. Appl., vol. 26, no. 3, pp. 161–170, 1992.
[81] F. Errico, G. Desaulniers, M. Gendreau, W. Rei, and L. M. Rousseau, “The vehicle routing problem with hard time windows and stochastic service times,” EURO J. Transp. Logist., vol. 7, no. 3, pp. 223–251, 2018. https://doi.org/10.1007/s13676-016-0101-4.
[82] P. Jaillet, “Probabilistic Traveling Salesman Problems,” Massachusetts Institute of Technology, 1985.
[83] P. Balaprakash, M. Birattari, T. Stützle, and M. Dorigo, “Estimation-based metaheuristics for the single vehicle routing problem with stochastic demands and customers,” Comput. Optim. Appl., vol. 61, no. 2, pp. 463–487, 2015. https://doi.org/10.1007/s10589-014-9719-z.
[84] P. Jaillet, “A-Priori solution of a traveling salesman problem in which a random subset of the customers are visited,” Oper. Res., vol. 36, no. 6, pp. 929–936, 1988. https://doi.org/10.1287/opre.36.6.929.
[85] N. A. Gelves-tello, R. Mora Moreno, and H. Lamos, “Solución del problema de ruteo de vehículos con demandas estocásticas mediante la optimización por espiral,” Fac. Ing., vol. 25, no. 42, pp. 7–19, 2016.
[86] T. Dinh, R. Fukasawa, and J. Luedtke, Exact algorithms for the chance-constrained vehicle routing problem, vol. 172, no. 1–2. Springer Berlin Heidelberg, 2018. https://doi.org/10.1007/s10107-017-1151-6.
[87] B. Yao, C. McLean, and H. Yang, “Robust optimization of dynamic route planning in same-day delivery networks with one-time observation of new demand,” Networks, vol. 73, no. 4, pp. 434–452, 2019. https://doi.org/10.1002/net.21890.
[88] A. Gutierrez, L. Dieulle, N. Labadie, and N. Velasco, “A multi-population algorithm to solve the VRP with stochastic service and travel times,” Comput. Ind. Eng., vol. 125, pp. 144–156, 2018. https://doi.org/10.1016/j.cie.2018.07.042.
[89] D. R. Gaur, A. Mudgal, and R. R. Singh, “Improved approximation algorithms for cumulative VRP with stochastic demands,” Discret. Appl. Math., pp. 1–11, 2018. https://doi.org/10.1016/j.dam.2018.01.012.
[90] A. Gutierrez, L. Dieulle, N. Labadie, and N. Velasco, “A hybrid metaheuristic algorithm for the vehicle routing problem with stochastic demands,” Comput. Oper. Res., vol. 99, pp. 135–147, 2018. https://doi.org/10.1016/j.cor.2018.06.012.
[91] D. Guimarans, O. Dominguez, J. Panadero, and A. A. Juan, “A simheuristic approach for the two-dimensional vehicle routing problem with stochastic travel times,” Simul. Model. Pract. Theory, vol. 89, pp. 1–14, 2018. https://doi.org/10.1016/j.simpat.2018.09.004.
[92] M. W. Ulmer, J. C. Goodson, D. C. Mattfeld, and M. Hennig, “Offline–online approximate dynamic programming for dynamic vehicle routing with stochastic requests,” Transp. Sci., vol. 53, no. 1, pp. 185–202, 2019. https://doi.org/10.1287/trsc.2017.0767.
[93] D. M. Miranda, J. Branke, and S. V. Conceição, “Algorithms for the multi-objective vehicle routing problem with hard time windows and stochastic travel time and service time,” Appl. Soft Comput. J., vol. 70, pp. 66–79, 2018. https://doi.org/10.1016/j.asoc.2018.05.026.
[94] Y. Shi, T. Boudouh, O. Grunder, and D. Wang, “Modeling and solving simultaneous delivery and pick-up problem with stochastic travel and service times in home health care,” Expert Syst. Appl., vol. 102, pp. 218–233, 2018. https://doi.org/10.1016/j.eswa.2018.02.025.
[95] F. V. Louveaux and J. J. Salazar-González, “Exact approach for the vehicle routing problem with stochastic demands and preventive returns,” Transp. Sci., vol. 52, no. 6, pp. 1463–1478, 2018. https://doi.org/10.1287/trsc.2017.0780.
[96] F. Lagos, M. A. Klapp, and A. Toriello, “Branch-and-Price for Routing with Probabilistic Customers,” pp. 1–31, 2018.
[97] M. Salavati-Khoshghalb, M. Gendreau, O. Jabali, and W. Rei, “A Rule-Based Recourse for the Vehicle Routing Problem with Stochastic Demands,” Transp. Sci., vol. 53, no. 5, pp. 1334–1353, 2019. https://doi.org/10.1287/trsc.2018.0876.
[98] V. Baradaran, A. Shafaei, and A. H. Hosseinian, “Stochastic vehicle routing problem with heterogeneous vehicles and multiple prioritized time windows: Mathematical modeling and solution approach,” Comput. Ind. Eng., vol. 131, pp. 187–199, 2019. https://doi.org/10.1016/j.cie.2019.03.047.
[99] J. Oyola, H. Arntzen, and D. L. Woodruff, “The stochastic vehicle routing problem, a literature review, Part II: solution methods,” EURO J. Transp. Logist., vol. 6, no. 4, pp. 349–388, 2017. https://doi.org/10.1007/s13676-016-0099-7.
[100] F. Rayat, M. M. Musavi, and A. Bozorgi-Amiri, “Bi-objective reliable location-inventory-routing problem with partial backordering under disruption risks: A modified AMOSA approach,” Appl. Soft Comput. J., vol. 59, pp. 622–643, 2017. http://dx.doi.org/10.1016/j.asoc.2017.06.036.
